Régression Linéaire comment faire avec Keras

Dans cet article on voit comment faire la base du Machine Learning : la Régression Linéaire ! Pour ça on va utiliser la librairie Keras.

Mais avant ça, qu’est-ce qu’une régression linéaire ?

La régression linéaire est une approche permettant de résoudre un problème.

Prenons un exemple.

Nous avons récupérer des données sur l’ensemble d’une population :

• l’âge de chaque individu
• leur frais d’assurance santé

Si l’on affiche ces données sur un graphique voilà le résultat :

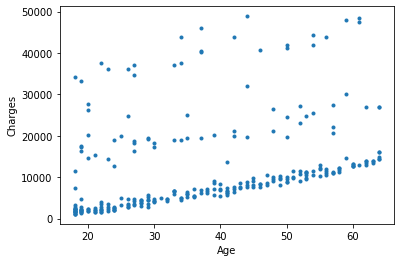
On appelle ça un nuage de points.

Ici, L’objectif de la régression linéaire est de trouver une relation mathématique entre l’âge et les frais d’assurance de cette population.

Un exemple de relation serait : plus l’âge d’un individu augmente, plus ses frais d’assurance santé augmente.

Cette relation doit être linéaire, c’est à dire qu’elle doit pouvoir être expliquer comme une equation y = ax+b.

x étant l’âge de l’individu et y étant les frais d’assurance.

Voilà un exemple de régression linéaire (droite orange) :

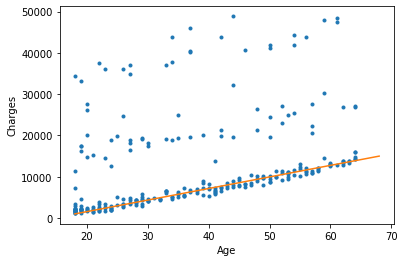
L’équation ci-dessus est : y = 280x-4040

Si un individu a 20 ans, ses frais sont égaux à 280*20-4040 = 1560

Néanmoins cela ne fonctionne pas pour tous les individus.

On peut voir sur le graphique que la droite orange (régression linéaire) ne passent PAS par tout les points.

La régression linéaire ne donne pas une résolution parfaite du problème. Elle ne permet pas de prédire tous les points.

MAIS, elle donne une solution optimale.

Optimale car on arrive à prédire la plupart des points avec cette droite de régression linéaire.

Cela en fait une solution rapide et adapté à beaucoup de problème.

Passons au Deep Learning avec Keras !

Régression Linéaire (Multiple)

Dans une régression linéaire classique on prendre une donnée (l’âge) pour en expliquer une autre (les frais d’assurance).

Mais en Deep Learning, l’opération est souvent plus corsée.

Dans notre cas on va devoir prendre plusieurs données pour en expliquer une autre.

Commençons par importer le dataset :

!git clone https://github.com/tkeldenich/datasets.git

On peut le lire avec la librairie Pandas :

import pandas as pd

df = pd.read_csv('datasets/insurance.csv') 
df.head()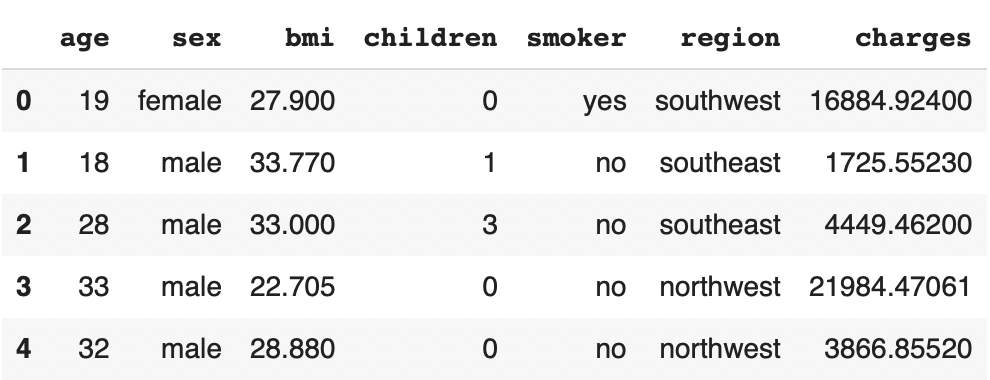

L’objectif dans ce problème est d’utiliser l’âge, le sexe, le BMI, le nombre d’enfant, le fais d’être fumeur ou non et la région d’habitation (données de prédictions) d’individus pour prédire leurs charges d’assurance santé (données à prédire).

C’est ce qu’on appelle une Régression Linéaire Multiple car on prend plusieurs variables pour en expliquer une autre.

Beaucoup de ces données sont des variables catégoriques.

Par exemple le sexe a deux options :

• male
• female

Au lieu d’avoir ces données sous forme de texte, transformons les en chiffres :

• 0
• 1

On applique cette transformation en mettant le résultat dans une nouvelle variable X :

X = pd.DataFrame()
df.sex = pd.Categorical(df.sex)

X['sex'] = df.sex.cat.codes

On affiche le résultat :

X.head()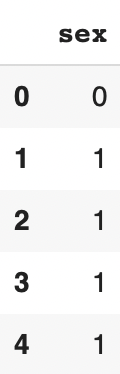

La transformation catégorie texte => catégorique chiffrée fonctionne.

Appliquons-la au reste de nos données catégoriques :

df.smoker = pd.Categorical(df.smoker)
df.region = pd.Categorical(df.region)

X['smoker'] = df.smoker.cat.codes
X['region'] = df.region.cat.codes

On a maintenant toutes nos données catégorique dans la variable X.

Transvasons le reste des données de prédictions dans cette même variable :

X['age'] = df['age']
X['bmi'] = df['bmi']

On a maintenant toutes nos données de prédictions dans la variable X. Affichons-les :

X.head()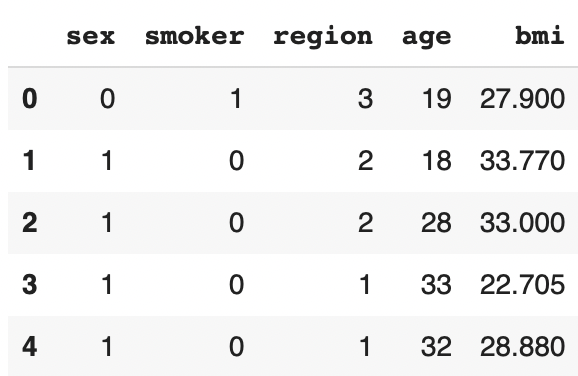

X_train, X_test, Y_train, Y_test

Il ne nous manque plus que les données à prédire Y :

Y = df['charges']

On a les X et les Y.

On sépare maintenant les données d’entraînement et de test :

from sklearn.model_selection import train_test_split

X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.20)

Nos données sont prêtes !

On peut passer aux choses sérieuses avec le Deep Learning.

IMPORTANT : Si tu ne comprends pas ce que sont les données X et Y et/ou les données d’entraînement et de test, je t’invite à lire cet article d’introduction à Keras ou bien à t’inscrire par email pour apprendre la méthode PARÉ pour faire du Deep Learning. Tu peux t’inscrire dans la case en milieu et fin d’article.

Modèle de Régression Linéaire avec Keras

Pour faire une Régression Linéaire (Multiple) avec Keras, on a besoin d’importer :

from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense

Si tu es débutant tu peux essayer avec deux simples couches Dense, comme ceci:

model = Sequential()
model.add(Dense(64, input_dim = 5))
model.add(Dense(1))

On compile :

model.compile(optimizer = 'adam', loss = 'mean_squared_error', metrics = ['mse', 'mae'])

Pour la compilation⬆ la régression linéaire nous donne une dernière contrainte : la loss function doit être la Mean Squared Error.

Elle permet de calculer l’erreur entre notre prédiction et le résultat réelle.

L’erreur est en quelque sorte une distance entre nos deux données.

Plus la prédiction est éloignée du résultat réelle, plus le modèle doit s’améliorer.

Autre chose, pour les metrics j’ai choisis d’afficher ici la mse (Mean Squared Error) et la mae (Mean Absolute Error).

À chaque erreur, on pourra voir comment les résultats évoluent.

L’idée c’est que plus le modèle s’optimise, plus l’erreur doit diminuer.

Entraînement

On peut entraîner le modèle :

history = model.fit(X_train, Y_train, validation_split=0.2, epochs=200)

On voit ici les résultats MSE et MAE.

Les deux évoluent de manière similaire. Quand l’une augmente, l’autre augmente. Quand l’une diminue, l’autre diminue.

On a donc les mêmes informations sur ces deux métriques.

MAIS, je préfère regarder le score de MAE. Ce dernier étant beaucoup plus proche de nos valeurs de frais d’assurance.

Je m’explique.

En regardant la MSE sur la dernière ligne, on voit 28.009.306. Ce score n’a aucun sens pour nous. Aucune de nos variables semble liés à un score aussi élevé. Par contre il a du sens pour le modèle de Deep Learning qui l’utilise pour s’optimiser !

Cependant, en regardant la MAE sur la dernière ligne, on voit 3.299,4. Ce score a beaucoup plus de sens ! Il semble liés à nos données de frais d’assurances.

Il faut interpréter la MAE comme suis : si le score est de 3.299,4 cela veut dire que lorsqu’on prédit les frais d’assurance d’un individu, l’erreur moyenne est de 3.299,4.

Exemple, on prédit pour Mr. Paul 33 ans, des frais d’assurance à 13.299,4$ alors que la valeur réelle est de 10.000$.

Le score prédit est relativement proche de la valeur réelle.

L’objectif est de minimiser cette distance.

Je parle plus en détails de la MAE dans la méthode PARÉ tu peux t’y inscrire gratuitement en milieu et fin d’article si ça t’intéresse 😉

Ce qu’il faut retenir : la MSE est utilisée par l’algorithme pour s’optimiser, la MAE est utilisée par le Data Scientist/Engineer/etc pour mesurer la performance du modèle.

Allons plus loin dans l’analyse du résultat !

Comprendre les résultats avec des KPI

Commençons par afficher l’évolution de la MAE au cours de l’entraînement :

import matplotlib.pyplot as plt

#plot the loss and validation loss of the dataset
plt.plot(history.history['mae'], label='mae')
plt.plot(history.history['val_mae'], label='val_mae')

plt.legend()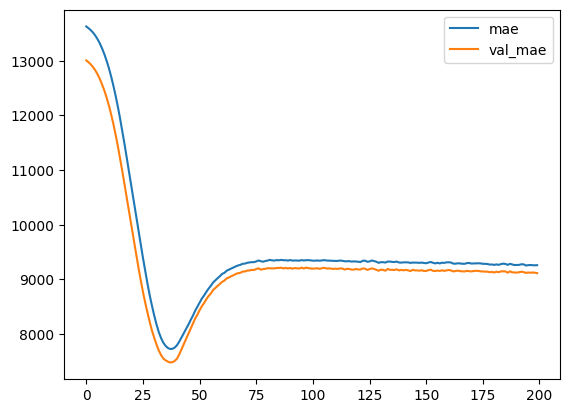

L’évolution est bonne, il n’y a pas d’événement inhabituelle, la diminution est régulière et la valeur de validation suis la valeur d’entraînement.

Encore une fois, si tu ne comprends pas l’analyse de cette courbe, je t’invite a voir cet article sur les bases du Deep Learning avec Keras.

Maintenant on veut analyser notre modèle sur des données qu’il n’a jamais vu : les données de test…

scores = model.evaluate(X_test, Y_test, verbose = 0)

print('Mean Squared Error : ', scores[1])
print('Mean Absolute Error : ', scores[2])

Mean Squared Error : 41.614.964,0
Mean Absolute Error : 4.095,5

Ici aussi je m’intéresse uniquement à la MAE.

Le résultat semble bon ! Il n’y a qu’une légère différence entre le résultat sur les données d’entraînement (3.299,4) et les données de test (4.095,5).

R2 score

On utilise une dernière mesure pour vraiment se faire une idée du résultat du modèle.

Tout d’abord on récupère toutes les prédictions sur les données de test :

Y_pred = model.predict(X_test)

Puis on les compare aux données réelles

Pour cela on utilise le R2 score.

Le R2 Score nous donne un taux de précision.

L’avantage par rapport à la MAE c’est qu’il nous donne un objectif beaucoup plus clair.

Avec la MAE l’objectif est de se rapprocher de 0. Mais dans notre cas une erreur de 100, 500, 1.000, voir 3.000$ est acceptable.

Par exemple si on prédit les frais d’assurance de Mme Lapie à 46.000$ alors qu’ils sont en réalité à 45.000$, l’erreur est minime.

C’est parce que : plus les frais d’assurance sont élevés moins l’erreur a d’impact.

Si par contre, l’objectif est de prédire le prix d’un stylo à 3$ et que l’erreur est de 1.000$… là, il y a un gros problème.

En fait la MAE doit être considérer en fonction de l’échelle de valeurs de Y.

La MAE doit tendre vers zéro. Mais si l’objectif est élevé, la MAE peut être considérée comme bonne même quand elle est élevé.

Avec la MAE il faut avoir en tête l’échelle de valeurs de Y.

Mais avec le R2 score, il n’y a pas besoin !

Le R2 score, donne résultat qui se conforme naturellement à l’échelle de valeur de Y.

Il nous donne un taux de précision.

On le calcul grâce à la librairie SKLearn :

from sklearn.metrics import r2_score

print('r2 score: ', r2_score(Y_test, Y_pred))

Sortie : 0.73

Notre précision est 73%, c’est une précision acceptable mais qui peut être améliorer !

Ici, on peut décider que : obtenir un résultat proche de 85% / 90% est un bon score.

Comprendre les résultats visuellement

Terminons avec l’interprétation des résultats sans métrique, seulement visuellement.

Tout d’abord on peut voir les résultat 1 par 1 :

Y_pred[:5]

4536.7
3526.3
2121.1
3986.7
14031.6

Et les comparer aux valeurs réelles :

Y_test.head()

23288.9
1909.5
1719.4
2166.7
11365.9

Je te laisse analyser par toi-même ces résultats, tu peux mettre ta réponse en commentaire.

Ensuite, la partie la plus intéressante car la plus visuelle !

Je te propose d’afficher chacune des valeurs prédites en fonction des valeurs réelles :

Y_pred = model.predict(X_test).flatten()

a = plt.axes(aspect='equal')
plt.scatter(Y_test, Y_pred)
plt.xlabel('True values')
plt.ylabel('Predicted values')
plt.xlim([0, 50000])
plt.ylim([0, 50000])
plt.plot([0, 50000], [0, 50000])
plt.plot()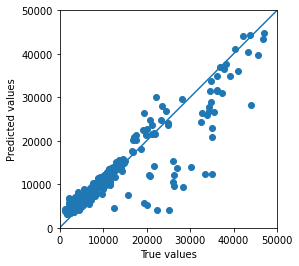

Ici nous avons une droite centrale.

Plus les points se rapproche de la droite, plus la prédiction est bonne.

Pourquoi ?

Car un point est sur la droite lorsque la valeur prédite est égale à la valeur réelle.

Exemple, si la valeur prédite est de 10.000 et que la valeur réelle est elle aussi de 10.000, le point se retrouvera exactement sur la droite.

Plus il y a de points se rapprochant de la droite, plus le modèle est précis.

Ici on ne voit que quelques points étant très éloignés de la droite. Cela veut dire que le modèle a une bonne précision.

Conclusion

À retenir, pour faire une Régression Linéaire (Multiple):

• Transformer vos données catégorique textuel en chiffre
• Ne pas mettre de fonction d’activation dans la dernière couche de votre modèle
• Utiliser la Mean Squared Error (mse) en loss
• Utiliser la Mean Absolute Error (mae) en metrics
• Le R2 score vous permet d’avoir un objectif d’optimisation claire
• Afficher les données prédites en fonctions des données réelles vous permet d’analyser visuellement vos résultat

Maintenant il ne vous reste plus qu’à optimiser votre modèle !

On explique les bonnes techniques dans les articles suivants :

• Normaliser ses données
• La Cross-Validation
• Changer les hyperparamètres des modèles

À bientôt sur Inside Machine Learning ! 🔥