Voyons en détails ce qu’est la formule de Pearson, ou coefficient de corrélation linéaire, et comment la coder en Python sans aucune librairie !
En mathématique, la corrélation entre plusieurs variables implique que ces variables sont dépendantes entre elles.
La corrélation linéaire, elle, implique que deux variables ont une relation linéaire entre elles. S’il y a corrélation linéaire alors on peut représentée par une droite la relation entre ces variables.
Pour calculer cette coefficient corrélation linéaire, on utilise la formule de Pearson qui est la calcul de la covariance entre les variables, diviser par le produit de leurs écarts types.
Ainsi, si l’on veut calculer la corrélation linéaire entre deux variables on utilisera :
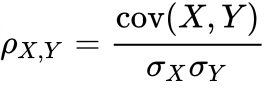
Plus la valeur absolue du coefficient de corrélation linéaire est élevé, plus les deux variables sont corrélées linéairement (i.e plus la relation peut être représentée par une droite.)
Cependant un coefficient nul n’implique pas indépendance, car d’autres types de corrélation (non linéaire) sont possibles.
Cette formule est notamment aborder dans l’exercice du site HackerRank pour l’entraînement en Statistiques & Machine Learning : Correlation and Regression Lines – A Quick Recap #1
La formule de Pearson
Tout d’abord on a nos deux variables, deux listes d’entiers :
Au fait, si ton objectif est d'apprendre le Deep Learning - j’ai préparé pour toi le Plan d’action pour Maîtriser les Réseaux de neurones.
7 jours de conseils gratuits d’un ingénieur spécialisé en Intelligence Artificielle pour apprendre à maîtriser les réseaux de neurones à partir de zéro :
- Planifie ton apprentissage
- Structure tes projets
- Développe tes algorithmes d’Intelligence Artificielle
J’ai basé ce programme sur des faits scientifiques, des approches éprouvées par des chercheurs mais également mes propres techniques que j'ai conçues au fil de mes expériences dans le domaine du Deep Learning.
Pour y accéder, clique ici :
À présent, on peut revenir à ce que je mentionnais précédemment.
x = [15, 12, 8, 8, 7, 7, 7, 6, 5, 3]
y = [10, 25, 17, 11, 13, 17, 20, 13, 9, 15]On calcule la moyenne de ces variables…
mX = sum(x)/len(x)
mY = sum(y)/len(y)… pour calculer ensuite la covariance :
cov = sum((a - mX) * (b - mY) for (a,b) in zip(x,y)) / len(x)Ensuite on calcule l’écart-type (en anglais standard deviation) de chacune des variables :
stdevX = (sum((a - mX)**2 for a in x)/len(x))**0.5
stdevY = (sum((b - mY)**2 for b in y)/len(y))**0.5Puis on peut calculer le coefficient de corrélation linéaire grâce à la formule de Pearson !
(On a intentionnellement arrondit le résultat à trois chiffres après la virgule)
result = round(cov/(stdevX*stdevY),3)Finalement, on affiche le résultat :
print(result)On obtient 0.145, cela implique que les deux variables ne sont pas vraiment corrélées linéairement !
sources :
- Wikipedia
- Photo by Everton Vila on Unsplash
Un dernier mot, si tu veux aller plus loin et apprendre le Deep Learning - j’ai préparé pour toi le Plan d’action pour Maîtriser les Réseaux de neurones.
7 jours de conseils gratuits d’un ingénieur spécialisé en Intelligence Artificielle pour apprendre à maîtriser les réseaux de neurones à partir de zéro :
- Planifie ton apprentissage
- Structure tes projets
- Développe tes algorithmes d’Intelligence Artificielle
J’ai basé ce programme sur des faits scientifiques, des approches éprouvées par des chercheurs mais également mes propres techniques que j'ai conçues au fil de mes expériences dans le domaine du Deep Learning.
Pour y accéder, clique ici :