Arbre de Décision Comment l’Utiliser – Meilleur Tutoriel

Voyons en détails comment fonctionne l’Arbre de Décision avec Scikit-Learn et surtout comment l’utiliser et l’améliorer !

Le Decision Tree, aussi appelé Arbre de Décision, est un algorithme de Machine Learning permettant de classifier des données en se basant sur des suites de conditions.

Dans cet article on va voir comment fonctionne l »Arbre de Décision.

C’est un modèle performant qui nous a permis, dans notre article pour apprendre le Machine Learning, d’atteindre une précision de 60%. Ainsi le Decision Tree est le modèle qui nous a donné le plus haut taux de réussite.

Après avoir compris ce qu’est un Arbre de Décision, on analysera les différents hyperparamètres qu’il propose.

Arrivera-t-on à améliorer notre Arbre de Décision en modifiant les hyperparamètres ? C’est ce qu’on va voir dans cet article !

Charger les data

Ici, nous allons reprendre les même données que dans notre article sur le Machine Learning. Si vous ne l’avez pas encore lu et que vous avez les bases du Machine Learning, vous pourrez tout de même comprendre ce tutoriel.

On importe tout d’abord nos datasets :

!git clone https://github.com/tkeldenich/datasets.git

Le dataset qui nous intéresse est le winequality-white.csv.

On peut l’ouvrir avec la librairie Pandas et l’afficher :

import pandas as pd

df = pd.read_csv("/content/datasets/winequality-white.csv", sep=";")
df.head(3)

Nous avons 7 features pour 1 label.

L’objectif est de prédire la qualité des vins en fonction des features.

On peut directement créer X_train, X_test, y_train, y_test pour l’entraînement du modèle.

from sklearn.model_selection import train_test_split

features = df.drop(['quality'], axis=1)
labels = df[['quality']]
X_train, X_test, y_train, y_test = train_test_split(features, labels, test_size=0.2)

Maintenant que le dataset est chargé, passons à ce qui nous intéresse vraiment : l’Arbre de Décision.

Comprendre l’Arbre de Décision

En théorie

L’Arbre de Décision s’utilise lors d’une tâche de classification.

Dans notre cas, on l’utilise pour classer des vins parmi 7 niveaux de qualité : [3, 4, 5, 6, 7, 8, 9]

L’algorithme de l’Arbre de Décision analyse nos données. Il se base sur les features (fixed acidity, volatile acidity, citric acid, residual sugar, chlorides, free sulfur dioxide, total sulfur dioxide, density, pH, sulphates, alcohol, quality) pour prédire à quelle classe appartient chaque vin.

Il commence avec le feature que son algorithme trouve le plus pertinent, et crée deux sous groupe.

Par exemple, s’il analyse que les vins de qualité 3 ont un taux d’alcool inférieur à 7%, il peut créer deux sous groupe : le groupe des vins inférieur à 7% (et de qualité 3) et les groupes de vins supérieur à 7% (et de qualité 4, 5, 6, 7, 8, 9).

Ainsi le taux d’alcool inférieur à 7% est un règle de décision pour discriminer nos données et les classifier.

L’Arbre de Décision continue ce processus jusqu’à obtenir des groupes qui correspondent le mieux possible à chacune de nos classes et ainsi classifier l’ensemble du dataset.

Cependant, dans la pratique, une règle ne permet pas forcément une discrimination parfaite de nos données.

Effectivement, il se peut que dans les vins avec un taux d’alcool inférieur à 7%, il n’y ait pas seulement des vins de qualité 3, mais aussi d’autres de qualité 4, 5.

Il faudra alors poursuivre la création de règle de discrimination sur ce groupe de données.

C’est ainsi qu’un Decision Tree peut se retrouver rapidement avec un nombre de règles important. Surtout si nos features sont complexes et peu corrélés avec nos labels comme le montre notre analyse du taux de corrélation entre nos features et nos labels.

Dans la pratique – Arbre de Décision

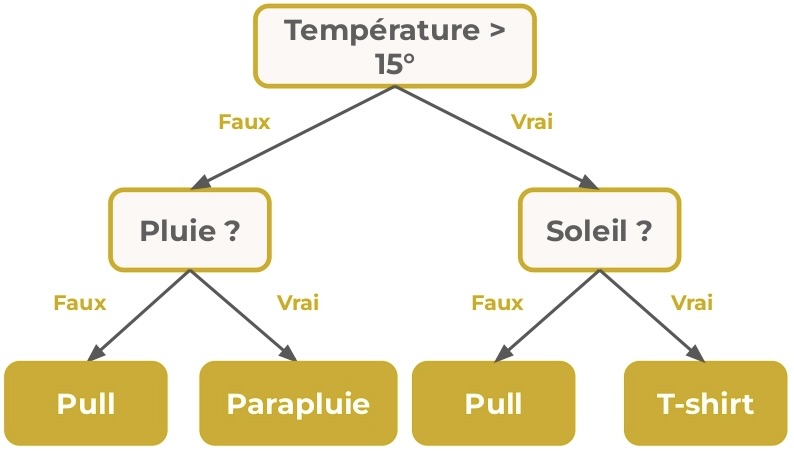
L’Arbre de Décision se compose de noeud, de branche et de feuilles.

Dans un noeud, l’algorithme teste un feature de notre dataset pour discriminer les données. C’est là qu’il crée une règle de discrimination.

Le test effectué a 2 résultat possibles : Vrai ou Faux.

Par exemple, dans notre cas, un test peut être : le taux d’alcool est-il supérieur à 7% ?

Dans les deux cas, l’arbre de decision créera deux chemin : Vrai et Faux.

C’est deux options créent deux branches qui amènent à un autre noeud où un autre test sera effectuer pour discriminer nos données.

Le premier noeud est appelé la racine.

Le noeud final d’une branche est appelé une feuille. Il signifie la prise de décision.

La profondeur d’un arbre est défini par la longueur du chemin le plus long entre une racine et une feuille.

L’arbre suivant a 3 noeud, 2 feuilles, 1 racine et une profondeur de 1 :

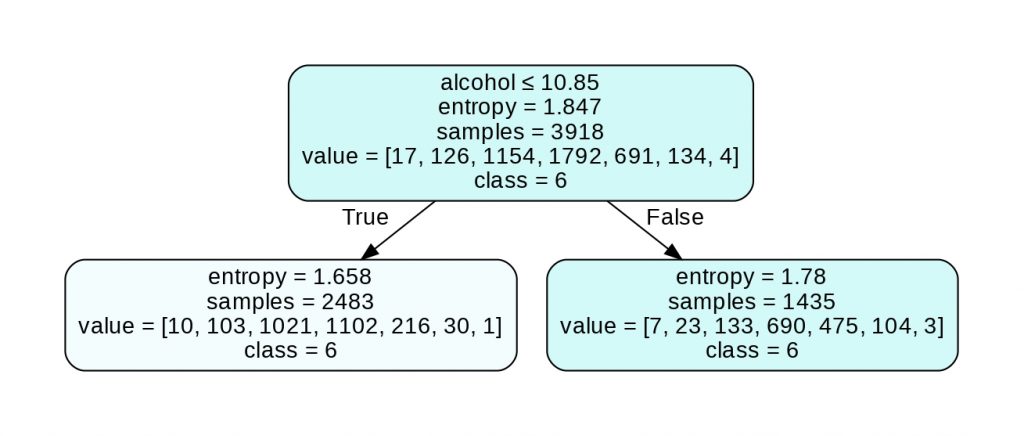
On a plusieurs informations dans cette arbre. Voyons cela en détail :

Premier attribut

Le premier attribut indique le feature (et la valeur de ce dernier) sur lequel s’est basé l’algorithme pour discriminer nos données.

Remarque : le premier attribut n’est pas présent dans les noeuds feuilles.

Criterion (entropy ou gini)

L’entropie (ou gini selon le choix de l’utilisateur, voir plus bas) est la mesure qui permet de quantifier l’incertitude sur la règle de discrimination utilisée.

Plus l’entropie est élevée, plus l’incertitude est grande. Au dessus de 1, l’incertitude est considérée élevée.

Avec une incertitude supérieur à 1, on a peu de chance de prédire les classes sur les sous-groupes créés. Attention cependant, cela ne veut pas dire que la règle de discrimination est mauvaise.

Effectivement, le Decision Tree calcule la discrimination qu’il lui permettra de faire la meilleur prédiction.

Cela indique plutôt que les sous-groupes créés auront besoin à leur tour d’une analyse pour déterminer une règle de discrimination et créer d’autres sous-groupes.

Samples

Samples représente le nombre de données appartenant au sous-groupe du noeud.

Value

Value représente le nombre de données pour chaque label dans le sous-groupe du noeud.

Par exemple, pour le noeud en bas à gauche avec value = [10, 103, 1021, 1102, 216, 30, 1], on a 10 vin de qualité 3, 103 vins de qualités 4, 1021 de qualité 5, etc.

Class

Class représente la décision prise si le noeud actuelle serait une feuille.

Le Decision Tree prend la decision qui lui donnera le plus haut taux de précision.

Pour le noeud racine, 1792 vins appartiennent à la classe 6. Tous les autres classes ont un nombre de vins inférieur. La décision optimale est donc de prédire la classe 6.

Par ailleurs, s’il y a un nombre égal de données pour chaque classe dans un noeud, le Decision Tree est programmé pour choisir la première classe de la liste des nombres égaux.

On peut remarquer que les deux feuilles nous donnent la même classe : 6 (ce qui explique la valeur d’entropie). Effectivement, nos données étant complexes, il nous faudra un Decision Tree avec une profondeur plus élevée pour discriminer toutes nos classes.

Arbre de Décision – les hyperparamètres

Le Decision Tree possède plusieurs hyperparamètres. Les plus basiques étant :

• criterion (« gini » ou « entropy ») – La fonction (« gini » ou « entropy ») a prendre en compte pour calculer l’incertitude sur la règle de discrimination utilisée.
• splitter (« best » ou « random ») – la stratégie utilisée pour choisir le feature sur lequel créer une règle de discrimination. La valeur par défaut est « best ». C’est-à-dire que pour chaque nœud, l’algorithme prend en compte tous les features et choisit celui avec le meilleur criterion. Si « random », un feature aléatoire sera pris en compte. La technique « random » est utilisée pour éviter l’overfitting.
• max_features (nombre entier) – Le nombre de feature à prendre en compte lors de la recherche du meilleur split (de la meilleure règle de discrimination).
• random_state (nombre entier) – permet de contrôler l’aléatoire dans l’algorithme. Si aucun chiffre n’est indiqué, l’algorithme lui en donne un au hasard à chaque nouvel entraînement. Cela aura pour effet de changer le résultat à chaque nouvel entraînement. Si un chiffre est indiqué, l’algorithme aura toujours le même résultat même après un nouvel entraînement.

Size attributes

Ensuite, on peut lister les paramètres agissant sur la taille de l’Arbre de Décision

• max_depth (nombre entier) – la profondeur maximale de l’arbre.
• min_samples_split (nombre entier) – Le nombre minimum de samples requis pour créer une règle de decision.
• min_samples_leaf (nombre entier) – Le nombre minimum de sample requis pour être à une feuille. Une feuille ne pourra pas avoir un nombre de sample inférieur à cette valeur. Idéal pour contrer l’overfitting.
• max_leaf_nodes (nombre entier) – Le nombre maximum de feuille que contient le Decision Tree.
• min_impurity_decrease (nombre entier) – La valeur minimum de diminution d’impureté requis pour créer une nouvelle règle de décision. Un nœud sera splitté si cette division induit une diminution de l’impureté supérieure ou égale à cette valeur. L’impureté est directement corrélé au criterion (ainsi, plus l’entropie diminue elle aussi, plus l’impureté diminue).

On peut initialiser notre Arbre avec deux hyperparamètres :

• criterion = « entropy »
• max_depth = 3

from sklearn import tree

decisionTree = tree.DecisionTreeClassifier(criterion="entropy",
                                           max_depth=3)

On entraîne l’Arbre :

decisionTree.fit(X_train, y_train)

Et calcule sa performance :

decisionTree.score(X_test, y_test)

Sortie: 0.504

50% de précision, on est loin de la performance atteinte dans notre article.

On peut afficher l’Arbre pour analyser le résultat :

import graphviz

labels_unique = labels.quality.unique().tolist()
labels_unique.sort()
labels_unique

dot_data = tree.export_graphviz(decisionTree, out_file=None,
                                feature_names=features.columns.to_list(),
                                class_names=[str(x) for x in labels_unique],
                                filled=True, rounded=True,
                                special_characters=True)
graph = graphviz.Source(dot_data)
graph.render("wine")
graph

On voit ici que l’Arbre de Décision n’a pas assez de feuilles pour prédire les classes 3, 8 et 9.

Effectivement le Decision Tree donne la priorité aux classes avec le plus grand nombre de vins. Ici, l’Arbre n’a pas encore eu le temps d’analyser les classes contenant le moins de vins.

Il nous faudra donc une profondeur plus élevée pour obtenir un bon Arbre de Décision.

Pruned Decision Tree

Le Pruning est une technique pour réduire la complexité d’un Arbre de Décision.

L’idée est de mesurer la pertinence de chaque noeud, puis de supprimer (de pruner) les moins critiques, et qui ajoute de la complexité inutilement.

Le Pruning est réalisé par le Decision Tree quand on indique une valeur à cette hyperparamètre :

ccp_alpha (nombre à virgule) – Le noeud (ou les noeuds) avec la complexité la plus grande et inférieur à ccp_alpha sera pruned.

Voyons ça en pratique :

from sklearn import tree

decisionTree = tree.DecisionTreeClassifier(criterion="entropy",
                                           ccp_alpha=0.015,
                                           max_depth=3  
                                           )

On entraîne l’Arbre :

decisionTree.fit(X_train, y_train)

Et calcule sa performance :

decisionTree.score(X_test, y_test)

Sortie: 0.496

Ici, on perd 0.8% de précision avec le Pruning mais c’est une technique qui vaut la peine d’être connu lorsque l’on souhaite réduire la complexité de l’Arbre de Décision.

Voilà son graphe associé :

import graphviz

labels_unique = labels.quality.unique().tolist()
labels_unique.sort()
labels_unique

dot_data = tree.export_graphviz(decisionTree, out_file=None,
                                feature_names=features.columns.to_list(),
                                class_names=[str(x) for x in labels_unique],
                                filled=True, rounded=True,
                                special_characters=True)
graph = graphviz.Source(dot_data)
graph.render("wine")
graph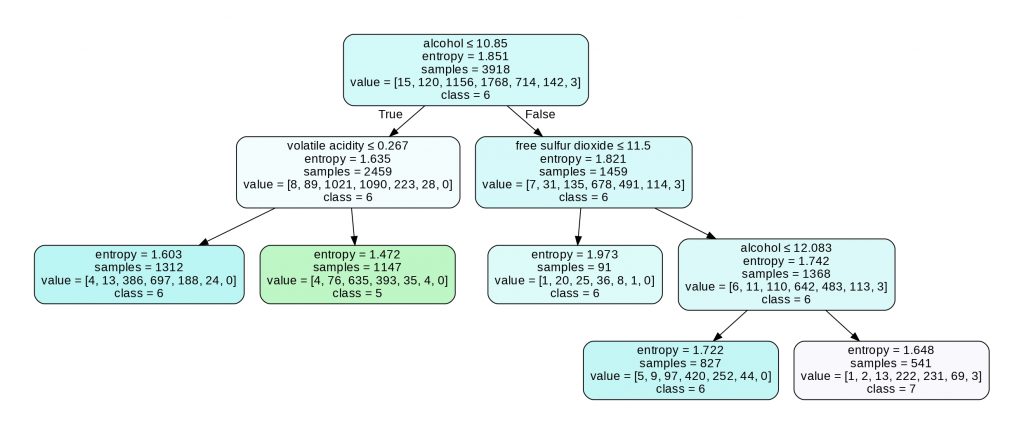

On peut voir ici que le Pruning à retiré 6 noeud qu’il considérait comme non-pertinent.

Weighted Decision Tree

Finalement, voyons l’hyperparamètre que je trouve le plus pertinent :

• class_weight (dictionnaire) – pendant le calcule du criterion, l’algorithme mesure l’impureté à travers toutes les classes du dataset. Il donne un poids égale pour chacune des classes. Mais en indiquant dans class_weight un poids différent pour chacune des classes, la statistique sera différente ce qui influencera le résultat final de l’algorithme.
• min_weight_fraction_leaf (nombre à virgule) – La fraction pondérée minimale de la somme totale des poids (de tous les échantillons d’entrée) requise pour être à un nœud feuille.

Ici je vous propose d’utiliser class_weight. Cela peut être une bonne option pour améliorer le modèle car le nombre de vins diffère grandement selon la classe.

Ainsi donner un poids différent aux classes permettra au criterion de prendre en considération la quantité de vin de chaque classe.

On indexe la valeur des poids en fonction du nombre de vin de la classe : {3:1, 4:2, 5:4, 6:5, 7:3, 8:2, 9:1}. La classe 3 a un poids de 1, la classe 4 a un poids de 2, etc.

Ainsi, plus le nombre de vins est élevé, plus le poids est important :

from sklearn import tree

decisionTree = tree.DecisionTreeClassifier(criterion="entropy",
                                           class_weight={3:1, 4:2, 5:4, 6:5, 7:3, 8:2, 9:1}
                                           )

On entraîne l’Arbre :

decisionTree.fit(X_train, y_train)

Et calcule sa performance :

decisionTree.score(X_test, y_test)

Sortie: 0.615

On atteint 61.5% de précision ! C’est 1.5% de plus qu’avant.

Cette « petite » amélioration est en fait une grosse avancée ! Effectivement dans le Machine Learning, la tâche la plus complexe est l’optimisation du modèle.

Améliorer les performances, ne serait-ce que d’1%, est déjà considérable !

Et vous, quel score avez-vous atteint ?

Cette méthode d’optimisation en changeant les hyperparamètres s’appelle : Hyperparameter Tuning.

Mais il existe bien d’autres techniques pour améliorer un modèle de Machine Learning :

• Normaliser nos données
• La Cross-Validation
• La Data Augmentation
• Les méthodes d’ensemble

Si vous souhaitez rester informé n’hésitez pas à vous abonnez à notre newsletter 😉