Ici, nous allons voir comment un réseau de neurones calcule la descente de gradient pour optimiser ses poids.
Cet article est la deuxième partie d’une suite de publication intitulée « Comment un modèle IA apprend ».
Dans la première partie, nous avons vu ce qu’est une loss function et pourquoi il faut la minimiser. Si tu veux consulter la première partie, clique ici.
Dans cette deuxième partie, nous allons explorer le concept de Descente de Gradient et comprendre son rôle dans l’apprentissage d’un modèle IA.
Avant d’aller plus loin, je te recommande d’être familiarisé avec le concept de tenseur, expliqué dans cet article.
Une fois ce concept en main, tu pourras aisément comprendre ce qui suit 🔥
Gradient
Dans la première partie, nous avons vu que pour optimiser un modèle il faut minimiser sa loss function et donc par corrélation optimiser ses poids.
Le problème qui se pose ici est de savoir:
- Si l’on doit augmenter ou diminuer les poids
- À quel point ces poids doivent être modifier.
Augmenter ou diminuer ? – Approximation Locale
Pour résoudre ce problème on va utiliser le gradient !
Le gradient est à une opération de tenseur ce que la dérivée est a une fonction.
On va donc prendre l’exemple d’une fonction et d’une dérivée pour bien comprendre le principe du gradient.
La dérivée nous permet de calculer l’approximation locale d’un point.
C’est grâce cette approximation locale que l’on peut savoir si x doit être augmenté ou diminué pour minimiser f(x).
Voilà, l’équation de l’approximation locale d’un point a:
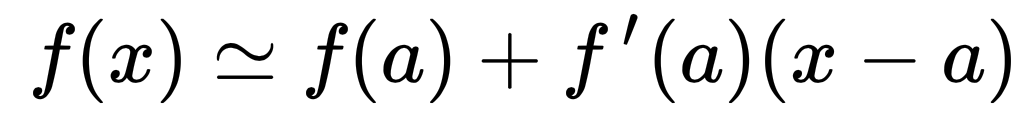
L’approximation locale d’une fonction permet de décrire l’évolution d’une fonction f(x) au voisinage de x.
Ainsi, si l’on veut réduire/minimiser f(x), il suffit de déplacer x dans la direction opposé à la croissance de la droite obtenue par approximation.
En fait, on va simplement se diriger vers le sens descendant de la pente.
Un exemple d’approximation locale de la fonction sinus en x = 2.
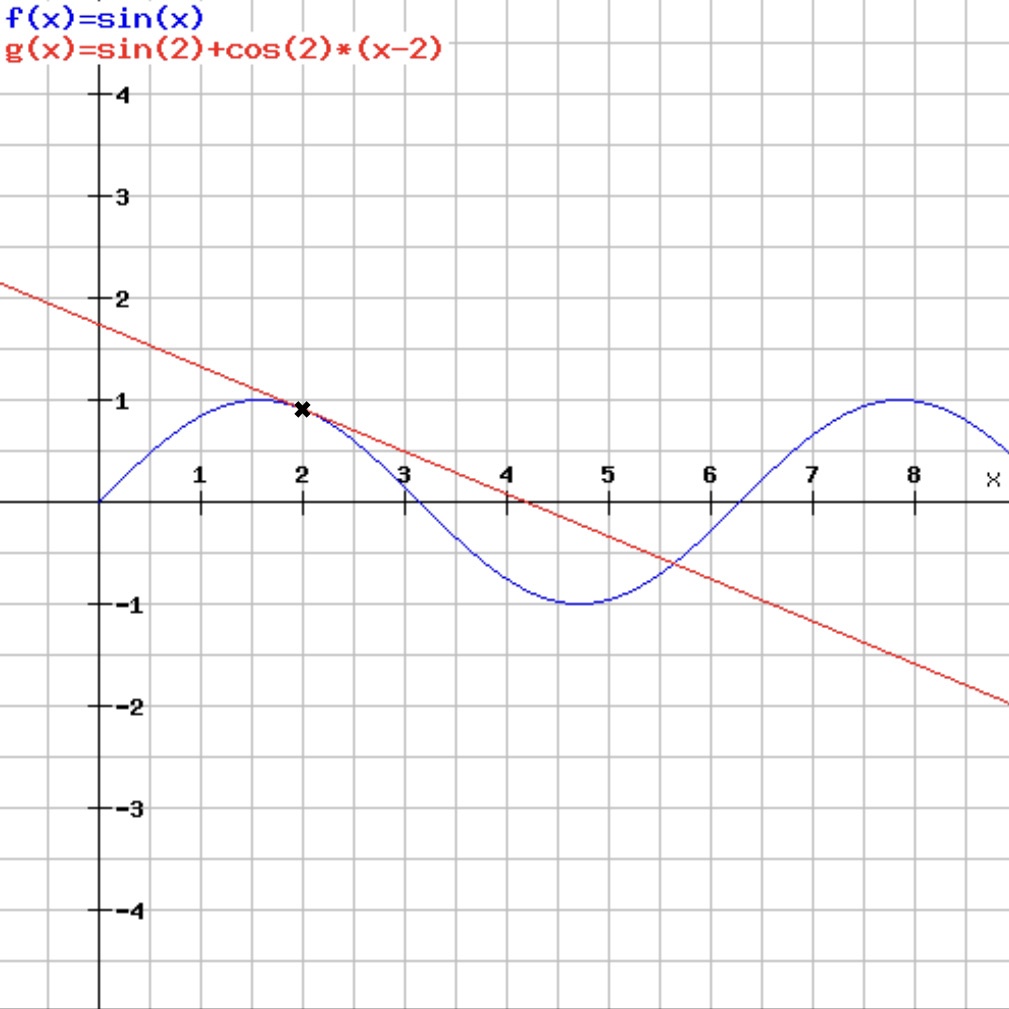
- Fonction sinus
- Approximation en 2
Sur ce schéma, l’approximation en 2 est une droite croissante si l’on se dirige à gauche du graphique.
On doit donc prendre la direction inverse.
Effectivement, f(x) est au minimum lorsque x = 5. Si l’on commence à x = 2, il faut donc se déplacer vers la droite, c’est-à-dire augmenter la valeur de x, pour minimiser f(x).
Grâce à l’approximation locale on détermine s’il faut augmenter ou réduire x. Mais il nous faut encore savoir…
À quel point le modifier ? – Descente de Gradient
Certes, dans notre exemple, il faut déplacer x vers la droite pour se rapprocher du minimum de f(x) mais nombre d’entre vous auront remarqué que s’il on augmente trop x on peut dépasser, distancer le minimum de f(x).
Au fait, si ton objectif est d'apprendre le Deep Learning - j’ai préparé pour toi le Plan d’action pour Maîtriser les Réseaux de neurones.
7 jours de conseils gratuits d’un ingénieur spécialisé en Intelligence Artificielle pour apprendre à maîtriser les réseaux de neurones à partir de zéro :
- Planifie ton apprentissage
- Structure tes projets
- Développe tes algorithmes d’Intelligence Artificielle
J’ai basé ce programme sur des faits scientifiques, des approches éprouvées par des chercheurs mais également mes propres techniques que j'ai conçues au fil de mes expériences dans le domaine du Deep Learning.
Pour y accéder, clique ici :
À présent, on peut revenir à ce que je mentionnais précédemment.
Si l’on augmente la valeur de x à x = 8 on se retrouve avec une valeur de f(x) supérieur à la valeur que l’on avait au début. Dans ce cas, on aura manqué notre optimisation.
C’est l’écueil qu’il faut éviter.
Optimiser nécessite d’être patient, ne pas viser la valeur optimal du premier coup. Il faut minimiser f(x) progressivement.
On va déplacer x graduellement vers le minimum et calculer l’approximation local après chaque déplacement. C’est ce qu’on appelle la descente de gradient.

De cette manière si on déplace x et qu’on se retrouve après le minimum de f(x) le calcul de l’approximation locale nous indiquera que l’on doit prendre la direction inverse pour se diriger à nouveau vers le minimum de f(x).
Pour effectuer la descente de gradient il faut déterminer deux paramètres :
- le pas (ou learning rate), la valeur qu’on ajoute à x, c’est-à-dire la distance qu’on parcours lors d’un déplacement
- le nombre d’itérations, le nombre de fois qu’on ajoute le pas à x, c’est-à-dire le nombre de fois que l’on déplace x
Il y a deux accrocs à éviter lors du choix des paramètres.
Si le pas est trop faible, la descente de gradient prendra de nombreuses itérations et il pourrait se bloquer dans un minimum local. Si le pas est trop grand, vos mises à jour peuvent finir par vous amener à des endroits complètement aléatoires de la courbe.
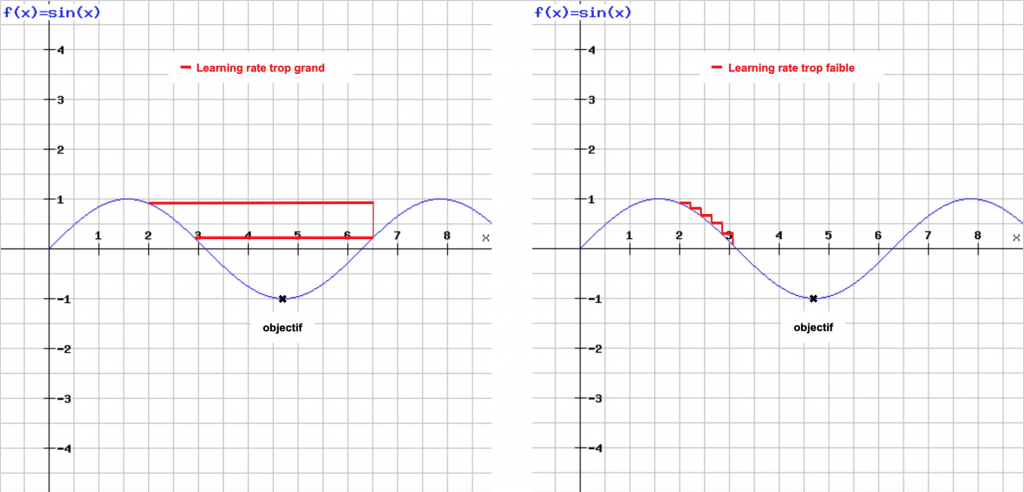
De même avec le nombre d’itérations, s’il est trop faible la descente de gradient n’aura pas le temps de se réaliser et le gradient ne sera pas optimiser. À l’inverse s’il est trop grand, cela rajoutera du temps aux calcul de l’optimisation du modèle et.. quand on fait du Deep Learning le temps est précieux.
Il est donc important de choisir des valeurs raisonnables pour ces deux paramètres afin qu’on optimise le calcul de la descente de gradient !
Backpropagation
Dans la pratique, une fonction de réseau de neurones est constituée de nombreuses opérations de tenseurs, chacune d’entre elles ayant une dérivée simple et connue.
Ces opérations de tenseurs sont composées, reliées entre elles pour former une fonction de réseau de neurones. C’est ce qu’on appelle une fonction composée.
Cette fonction composée peut être dérivée grâce à la règle de la chaîne. Il n’est pas nécessaire de connaître ce théorème pour comprendre ce qu’il se passe lors du Deep Learning mais pour les plus mathématiciens d’entre vous, il est expliqué sur cet article Wikipédia.
Appliquer la règle de la chaîne permet d’obtenir le gradient de la loss function par rapport à chaque poids. On calcule le gradient de chaque couche en commençant par la dernière couche et en finissant par la première. Cette application est appelée la Backpropagation.
Ainsi on peut calculer avec précision l’influence de chaque paramètre dans le résultat de la loss function et les modifier en conséquence.
Finalement, cela nous permet d’optimiser nos poids, minimiser la perte de la loss function et on peut enfin utiliser notre modèle de Deep Learning comme il se doit !

La Backpropagation se fait implicitement lors de l’entraînement d’un modèle et.. heureusement pour nous, il ne sera jamais nécessaire de l’implémenter !
Aujourd’hui, c’est grâce au Deep Learning que les leaders de la tech peuvent créer les Intelligences Artificielles les plus puissantes.
Si tu veux approfondir tes connaissances dans le domaine, tu peux accéder à mon Plan d’action pour Maîtriser les Réseaux de neurones.
Un programme de 7 cours gratuits que j’ai préparé pour te guider dans ton parcours pour apprendre le Deep Learning.
Si ça t’intéresse, clique ici :
Un dernier mot, si tu veux aller plus loin et apprendre le Deep Learning - j’ai préparé pour toi le Plan d’action pour Maîtriser les Réseaux de neurones.
7 jours de conseils gratuits d’un ingénieur spécialisé en Intelligence Artificielle pour apprendre à maîtriser les réseaux de neurones à partir de zéro :
- Planifie ton apprentissage
- Structure tes projets
- Développe tes algorithmes d’Intelligence Artificielle
J’ai basé ce programme sur des faits scientifiques, des approches éprouvées par des chercheurs mais également mes propres techniques que j'ai conçues au fil de mes expériences dans le domaine du Deep Learning.
Pour y accéder, clique ici :





Très bon article, pas chargé mais bien détaillé.