Optimisation Bayésienne – C’est quoi ? Comment l’utiliser ? – Meilleur Tutoriel

Dans cet article, je te dévoile les secrets de l’Optimisation Bayésienne, une technique révolutionnaire pour optimiser les hyperparamètres.

Les hyperparamètres jouent un rôle essentiel dans la performance des modèles de Machine Learning.

Cependant, trouver la combinaison optimal d’hyperparamètres peut être une tâche ardue. Cela nécessite souvent des analyses manuelles détaillées.

Mais quels sont exactement ces hyperparamètres ? Et comment l’optimisation bayésienne peut-elle révolutionner leur ajustement ?

Ici, je te propose d’explorer le concept de l’optimisation bayésienne, sa pratique au moyen de la bibliothèque bayes_opt en Python, et son impact sur la performance des modèles de Machine Learning.

Les Hyperparamètres

Qu’est-ce que les Hyperparamètres ?

Les hyperparamètres en Machine Learning sont des éléments configurables avant l’entraînement d’un modèle et qui influencent son comportement et sa performance.

Ils ne doivent pas être confondus avec les paramètres du modèle.

Ces derniers sont appris à partir des données lors de l’entraînement d’un modèle de Machine Learning et sont en constante évolution.

Des hyperparamètres communs sont: le learning rate, la profondeur d’un réseau de neurones ou encore le nombre de branche dans un Decision Tree.

En les choisissant judicieusement, il est possible que ton modèle de Machine Learning obtienne des performances élevés après son entraînement.

Le Défi de l’Ajustement Manuel (Manual Tuning)

Le choix des hyperparamètres peut avoir un impact significatif sur la performance d’un modèle.

Néanmoins, ajuster manuellement les hyperparamètres est une tâche chronophage.

Elle nécessite du temps et souvent, peut ne pas avoir l’effet attendu.

En effet, ajuster manuellement les hyperparamètres implique:

• exécuter de multiples expérimentations
• modifier itérativement les hyperparamètres
• évaluer la performance du modèle à chaque fin d’expérimentation

Ce processus peut être à la fois fastidieux et… inefficace ❌

Pour surmonter ces limites, il existe aujourd’hui (et depuis quelques années déjà) des techniques d’optimisation automatisées.

Ces méthodes visent à explorer progressivement l’espace des hyperparamètres à la recherche de la configuration optimale qui maximise la performance d’un modèle.

L’optimisation bayésienne est l’une de ces approches!🔥

L’Optimisation Bayésienne

Introduction à l’Optimisation Bayésienne

L’Optimisation Bayésienne en Machine Learning est une méthode d’optimisation qui utilise des modèles probabilistes pour trouver de manière efficace les hyperparamètres d’un modèle.

En d’autre termes, c’est une technique mathématique dont l’objectif est de trouver la combinaison d’hyperparamètres optimale.

Cette optimisation est réalisée en explorant de manière intelligente l’espace de recherche grâce à des modèles statistiques.

Pour cela, l’optimisation bayésienne utilise:

1. un modèle surrogate
2. une fonction d’acquisition
3. une stratégie d’équilibre entre exploration et exploitation

Principaux Composants de l’Optimisation Bayésienne

Le modèle surrogate (ou modèle de substitution) permet d’estimer la manière dont les différentes valeurs des hyperparamètres affectent les performances du modèle.

Il utilise les données des expérimentations précédentes pour prédire les performances potentielles de nouvelles combinaison d’hyperparamètres.

Ainsi, le modèle surrogate guide le choix des prochaines configurations à évaluer.

La fonction d’acquisition est une mesure mathématique qui évalue l’intérêt (ou l’utilité) d’évaluer une configuration d’hyperparamètres donnée.

Elle tient compte à la fois de l’incertitude du modèle surrogate et de la recherche d’une amélioration des performances du modèle.

Les fonctions d’acquisition couramment utilisées incluent:

• Expected Improvement
• Expected Optimism
• UCB – Upper Confidence Bound

La stratégie d’équilibre entre exploration et exploitation est l’approche utilisée pour décider si l’on doit explorer de nouvelles configurations d’hyperparamètres pour découvrir des améliorations potentielles (exploration) ou exploiter les configurations actuellement connues considérées comme étant les meilleures (exploitation).

Cette stratégie est essentielle pour trouver efficacement la meilleure combinaison d’hyperparamètres.

Pour réaliser cela, elle ajuste progressivement son approche pour choisir les prochaines combinaisons à évaluer en fonction de l’objectif d’optimisation.

Le Processus Itératif de l’Optimisation Bayésienne

En pratique, l’optimisation bayésienne se déroule itérativement :

1. Utiliser le modèle surrogate pour prédire la performance de différentes configurations d’hyperparamètres
2. Utiliser la fonction d’acquisition pour choisir la configuration d’hyperparamètres la plus prometteuse à évaluer ensuite
3. Évaluer la configuration d’hyperparamètres choisie
4. Mettre à jour le modèle surrogate avec les nouveaux résultats
5. Répéter le processus jusqu’à ce qu’un critère d’arrêt soit atteint, tel qu’un nombre maximal d’itérations ou un niveau de performance satisfaisant

La puissance de l’optimisation bayésienne réside dans sa capacité à utiliser un modèle pour faire des prédictions avisées sur les parties de l’espace des hyperparamètres à explorer.

Cette capacité peut réduire considérablement le nombre d’évaluations nécessaires pour trouver de bons hyperparamètres.

Une Bibliothèque pour faire de l’Optimisation Bayésienne bayes_opt

bayes_opt est une bibliothèque Python conçue pour exploiter facilement l’optimisation bayésienne.

Elle est compatible avec diverses bibliothèques de Machine Learning, y compris Scikit-learn et XGBoost. C’est donc un atout précieux pour les praticiens cherchant à optimiser leurs modèles.

Cette bibliothèque sert de pont entre les fondements théoriques de l’optimisation bayésienne et son application pratique.

Ainsi, elle adapte le processus d’optimisation à des tâches spécifiques en Machine Learning.

Voyons comment utiliser bayes_opt.

Utilisation de bayes_opt pour l’ajustement des Hyperparamètres

Avant d’utiliser la bibliothèque, il faut l’installer. Pour cela il suffit simplement d’utiliser la commande pip :

pip install bayesian-optimization==1.3.0

Remarque: pour ce tutoriel j’utilise la version 1.3.0 de la librairie.

Maintenant, prenons un exemple pratique en optimisant les résultats d’un modèle de Machine Learning.

Pour cet exemple, on imagine que l’on travaille sur un problème de classification en utilisant un classificateur Random Forest.

Dans ce contexte, nous avons plusieurs hyperparamètres à ajuster:

• n_estimators – le nombre d’arbres
• max_depth – la profondeur maximale des arbres
• min_samples_leaf – le nombre minimal d’échantillons par feuille

Voici un extrait de code Python montrant comment utiliser bayes_opt pour l’optimisation des hyperparamètres avec un classificateur Random Forest :

from bayes_opt import BayesianOptimization
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
from sklearn.model_selection import cross_val_score

# Définissez la fonction objectif à optimiser
def rf_cv(n_estimators, max_depth, min_samples_leaf):
    model = RandomForestClassifier(
        n_estimators=int(n_estimators),
        max_depth=int(max_depth),
        min_samples_leaf=int(min_samples_leaf),
        random_state=42,
    )
    # Utilisez la validation croisée pour estimer la performance
    scores = cross_val_score(model, X, y, cv=5, scoring='accuracy')
    return scores.mean()

# Créez un objet BayesianOptimization
bo = BayesianOptimization(
    f=rf_cv,
    pbounds={'n_estimators': (10, 200), 'max_depth': (2, 50), 'min_samples_leaf': (1, 10)},
    verbose=2
)

# Effectuez l'optimisation
bo.maximize(init_points=10, n_iter=50, acq='ucb')

# Meilleurs hyperparamètres et précision correspondante
best_params = bo.max['params']
best_accuracy = bo.max['target']

print(f"Meilleurs Hyperparamètres : {best_params}")
print(f"Meilleure Précision en Validation Croisée : {best_accuracy}")

La fonction rf_cv représente l’objectif. Ici, on souhaite optimiser la précision moyenne obtenue lors de la cross validation de notre modèle.

La variable pbounds définit l’espace de recherche à explorer pour sélectionner les hyperparamètres.

Pour que ce code fonctionne, il faudra avoir préalablement définit les variables X et y.

Si c’est ton cas, le résultat devra ressembler à cela:

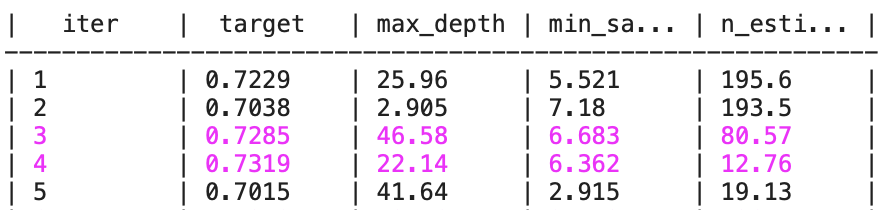
Meilleurs Hyperparamètres : {'max_depth': 29.597407514950014, 'min_samples_leaf': 8.786274398078726, 'n_estimators': 25.983234732342932}
Meilleure Précision en Validation Croisée : 0.7341095976398218

Voici ce que chaque colonne signifie dans ce tableau:

• iter : Il s’agit du numéro d’itération de l’optimisation bayésienne. Chaque itération représente une tentative de trouver de meilleurs hyperparamètres
• target : C’est la valeur de la fonction objectif, la métrique permettant d’évaluer le modèle (la précision moyenne obtenue lors de la cross validation)
• max_depth, min_samples_split, n_estimators : Ce sont les valeurs des hyperparamètres explorés lors de l’optimisation bayésienne

Remarque: les valeurs flottantes ayant étés attribuées à des hyperparamètres entiers, par exemple max_depth et n_estimator, sont arrondis lors de leur utilisation pour obtenir un entier.

À chaque itération, l’optimisation bayésienne tente une nouvelle combinaison d’hyperparamètres et enregistre la métrique de performance correspondante.

Quand, la combinaison d’hyperparamètres est meilleure que les précédentes, la ligne est affichée en violet.

Mais comment faire si l’on souhaite personnaliser bayes_opt pour des cas d’utilisation spécifiques ?

bayes_opt Personnalisation

L’un des avantages de bayes_opt est sa flexibilité. Voici quelques-unes des façons dont tu peux personnaliser l’outil pour l’adapter à des besoins spécifiques :

1. Définir une fonction objectif adaptée : Ta fonction objectif peut être adaptée à différents types de métriques telles que la precision, le recall, ou le F1-score selon les besoins de ton projet (des métriques que j’ai déjà détaillées dans cet article)
2. Utilisation de domaines d’hyperparamètres complexes : bayes_opt permet de spécifier des domaines non seulement numériques mais également catégoriels si nécessaire, grâce à des techniques comme l’encodage ou le mapping
3. Contraintes et conditions préalables : Tu peux intégrer des contraintes dans ton espace de recherche pour écarter des combinaisons non viables ou pour respecter certaines conditions préalables
4. Intégration avec des pipelines : bayes_opt peut être intégré dans des pipelines de traitement des données, te permettant d’optimiser non seulement les hyperparamètres du modèle mais aussi les étapes de prétraitement des données
5. Parallélisation de l’optimisation : Pour accélérer l’optimisation, bayes_opt peut être utilisé avec des outils de parallélisation pour exécuter plusieurs évaluations d’hyperparamètres simultanément
6. Sauvegarde et reprise : Il est possible de sauvegarder l’état de l’optimisation et de reprendre l’optimisation plus tard, ce qui est utile pour des processus d’optimisation très longs
7. Visualisation des résultats : bayes_opt peut être couplé avec des bibliothèques de visualisation pour suivre la progression de l’optimisation et analyser les résultats

Pour personnaliser bayes_opt, tu peut te plonger dans la documentation de la bibliothèque pour comprendre toutes les options disponibles.

Mais en attendant, voici un exemple de comment tu pourrais étendre le code existant pour inclure certaines de ces personnalisations :

Contraintes et conditions préalables

# Importez les bibliothèques nécessaires pour la personnalisation
from sklearn.ensemble import RandomForestClassifier
#from sklearn.metrics import accuracy_score
from sklearn.model_selection import cross_val_score
from bayes_opt import BayesianOptimization, UtilityFunction
import numpy as np

# Supposons que vous ayez un modèle complexe avec des préconditions, telles que:
# "max_depth" ne doit pas être inférieur à "min_samples_leaf"
def complex_model_cv(n_estimators, max_depth, min_samples_leaf):
    if max_depth < min_samples_leaf:
        return 0  # Une valeur de retour non favorable pour des combinaisons non viables
    else:
        model = RandomForestClassifier(
            n_estimators=int(n_estimators),
            max_depth=int(max_depth),
            min_samples_leaf=int(min_samples_leaf),
            random_state=42,
        )
        scores = cross_val_score(model, X, y, cv=5, scoring='accuracy')
        return scores.mean()

# Utilisez UtilityFunction pour personnaliser la fonction d'acquisition
acq = UtilityFunction(kind="ucb", kappa=2.5, xi=0.0)

# Définissez un objet BayesianOptimization avec des contraintes
pbounds = {'n_estimators': (10, 200), 'max_depth': (2, 50), 'min_samples_leaf': (1, 10)}

bo = BayesianOptimization(
    f=complex_model_cv,
    pbounds=pbounds,
    verbose=2,
)

# Utilisez la fonction d'acquisition personnalisée dans le processus d'optimisation
next_point_to_probe = acq.utility(bo.space.params_to_array(pbounds), bo._gp, bo._random_state)

Dans cette section de code, on initialise un processus d’optimisation bayésien pour un RandomForestClassifier en utilisant la bibliothèque bayes_opt.

Le modèle est défini avec certaines préconditions pour éviter des configurations non viables, par exemple, la profondeur maximale de l’arbre (max_depth) ne doit pas être inférieure au nombre minimal d’échantillons requis pour être à une feuille (min_samples_leaf).

Si ces conditions ne sont pas remplies, la fonction retourne 0, éliminant ainsi ces combinaisons d’hyperparamètres de la considération ultérieure.

La fonction d’acquisition, qui guide la sélection des prochains hyperparamètres à tester, est personnalisée avec UtilityFunction, ici en utilisant l’approche Upper Confidence Bound (UCB) avec des paramètres spécifiques kappa et xi.

Cela détermine l’équilibre entre l’exploitation des hyperparamètres connus pour bien performer et l’exploration de nouveaux hyperparamètres.

Un objet BayesianOptimization est ensuite créé avec les limites des hyperparamètres spécifiés dans pbounds.

Ces bornes définissent les plages de valeurs dans lesquelles l’optimisation doit rechercher les meilleurs hyperparamètres.

Enfin, on utilise la fonction d’acquisition personnalisée pour déterminer le prochain point à évaluer dans l’espace des hyperparamètres, ce qui est une étape essentielle dans l’itération du processus d’optimisation bayésienne.

Sauvegarde de l’optimisation

from bayes_opt.logger import JSONLogger
from bayes_opt.event import Events

# Sauvegarde de l'état de l'optimisation
logger = JSONLogger(path="./logs.log")
bo.subscribe(Events.OPTIMIZATION_STEP, logger)

bo.maximize(init_points=10, n_iter=50, acq='ucb')
params = bo.space.params
target = bo.space.target

Ce bloc de code illustre l’intégration d’un logger dans bayes_opt, permettant la sauvegarde automatique de l’état de l’optimisation après chaque étape.

Le logger est essentiel pour reprendre l’optimisation où elle s’est arrêtée, en particulier pour des processus d’optimisation qui peuvent prendre beaucoup de temps.

Ici, un JSONLogger est attaché à l’optimiseur bo pour enregistrer les événements dans un fichier log.

Après chaque étape d’optimisation, le meilleur ensemble d’hyperparamètres est mis à jour, et l’état actuel est sauvegardé, ce qui permet une récupération en cas d’interruption.

Visualisation des résultats

import matplotlib.pyplot as plt

# Visualisation de l'optimisation
plt.figure(figsize=(8, 2))
plt.scatter(params[:,0], target)
plt.title('N_estimators vs. Target')
plt.xlabel('N_estimators')
plt.ylabel('Target')
plt.show()

# Visualisation de la convergence de l'optimisation
plt.figure(figsize=(8, 2))
plt.plot(np.arange(len(bo.space)), target, '-o')
plt.title('Optimization Convergence')
plt.xlabel('Iteration')
plt.ylabel('Target')
plt.show()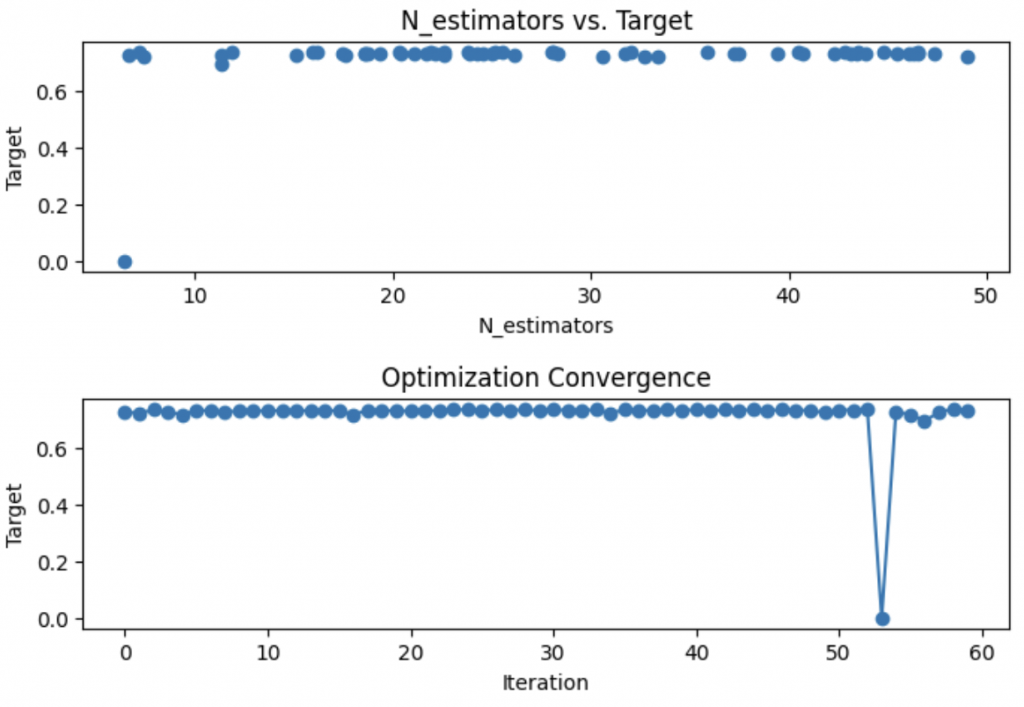

Dans ces lignes, nous visualisons les résultats de l’optimisation à l’aide de matplotlib.

Le premier graphique montre la relation entre le nombre d’estimateurs et la performance du modèle, aidant à identifier le nombre optimal d’estimateurs pour notre RandomForestClassifier.

Le deuxième graphique représente la convergence de l’optimisation au fil des itérations. Il permet de vérifier si l’optimisation progresse vers une meilleure solution ou si elle stagne. Selon le cas, cela pourrait indiquer le besoin d’ajuster le processus d’optimisation ou les hyperparamètres.

Reprise de l’optimisation

from bayes_opt.util import load_logs

# Définissez un objet BayesianOptimization avec des contraintes
new_bo = BayesianOptimization(
    f=complex_model_cv,
    pbounds=pbounds,
    verbose=2,
)

# Utilisez la fonction d'acquisition personnalisée dans le processus d'optimisation
next_point_to_probe = acq.utility(new_bo.space.params_to_array(pbounds), new_bo._gp, new_bo._random_state)

# Le nouvel optimiseur est chargé avec les points observés précédemment
load_logs(new_bo, logs=["./logs.log.json"]);

new_bo.maximize(init_points=0, n_iter=20, acq='ucb')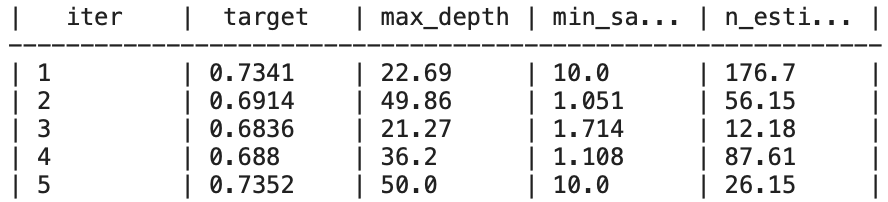

Ici, on charge l’état d’optimisation précédent dans un nouvel objet BayesianOptimization.

En utilisant la fonction load_logs, nous pouvons reprendre l’optimisation là où elle s’est arrêtée, en exploitant les informations recueillies précédemment.

Cela est particulièrement utile pour continuer l’optimisation sans perdre le progrès effectué après une interruption. Mais cela peut également être utile pour commencer l’optimisation avec un nouvel ensemble d’hyperparamètres basé sur les résultats précédents.

Aller plus loin

# Meilleurs hyperparamètres et précision correspondante après personnalisation
best_params_custom = new_bo.max['params']
best_accuracy_custom = new_bo.max['target']

print(f"Meilleurs Hyperparamètres après Personnalisation : {best_params_custom}")
print(f"Meilleure Précision en Validation Croisée après Personnalisation : {best_accuracy_custom}")

Sortie:
Meilleurs Hyperparamètres après Personnalisation : {'max_depth': 7.169316344372172, 'min_samples_leaf': 5.946827832091897, 'n_estimators': 34.972481159917464}
Meilleure Précision en Validation Croisée après Personnalisation : 0.7374866612265395

Le résultat affiche les meilleurs hyperparamètres obtenus après le processus d’optimisation avec bayes_opt. Il indique également la meilleure précision obtenue en utilisant la validation croisée.

On peut alors tirer une conclusion: l’optimisation bayésienne des hyperparamètres a un impact crucial la performance du modèle.

Le code détaillé ici montre comment:

• intégrer des contraintes dans ton espace de recherche avec bayes_opt
• personnaliser la fonction d’acquisition pour contrôler l’équilibre entre exploration et exploitation
• visualiser la progression et les résultats de l’optimisation
• sauvegarder et reprendre l’optimisation à un certain état d’exploration

En appliquant ce code de ton côté, tu verras que l’utilisation de bayes_opt fait des miracles!💫

Pour que tu puisses tester cela facilement – je te proposer d’accéder à un bonus.

À l’intérieur, tu retrouveras le code détaillé plus haut appliqué à un exemple concret.

Les données de cette expérimentation se téléchargerons automatiquement, et tu n’auras pas à recopier le code manuellement.

Tu pourras simplement l’importer dans Jupyter, Google Colab ou autre, et l’exécuter en un clic.

En plus de cela, tu accéderas à mon Plan d’action pour Maîtriser les Réseaux de neurones.

Un programme de 7 cours gratuits que j’ai préparé pour te guider dans ton parcours pour apprendre le Deep Learning.

Si le bonus et le programme t’intéresse, clique ici :

débloquer mon bonus !