Dans cet article, nous allons voir l’approche classique à utiliser pour faire de Classification Binaire en NLP.
La classification binaire est un problème de classification à deux options.
Pour cette classification binaire en NLP nous utilisons un jeu de données disponible dans la librairie Keras.
Ce jeu de données est composé :
- de critiques de films
- de labels (0 ou 1) associés à chaque critique
Les labels indiquent si la critique est positive (1) ou négative (0).
Le but de notre modèle de Deep Learning sera de déterminer à partir d’une critique de cinéma si le spectateur a aimé le film ou non. C’est-à-dire, si la critique est positive ou non.
Nous allons donc entraîner notre modèle sur des données d’entraînement puis le tester, vérifier ses capacités sur des données de test.
Préparer nos données – Classification Binaire NLP
Charger nos données
Premièrement, on charge les données depuis le package imdb.
train_data et train_labels sont les données sur lesquels on va entraîner notre modèle.
Il y a en tout 50 000 critiques et donc 50 000 labels. On entraîne notre modèle à prédire les labels à partir des critiques.
Ensuite on pourra tester l’efficacité du modèle en faisant des prédiction sur les test_data et en comparant ces prédictions de label au véritable label test_labels.
from keras.datasets import imdb
(train_data, train_labels), (test_data, test_labels) = imdb.load_data(num_words=10000)Les critiques de films (stockées dans train_data et test_data) on déjà était préprocesser, prétraiter.
C’est-à-dire que les critiques ont était transformées, encodées en chiffres.
Ainsi, une phrase est représentée par une liste de chiffres.
Chaque chiffre représente un mot.
num_words=10000 veut dire qu’on a gardé les 10 000 mots les plus fréquents dans l’ensemble des critiques.
On a donc une liste index de 10 000 mots et chaque numéro dans les critiques fait référence à un des mots de cette liste index.
Si une phrase contient le mot numéro 15, pour le connaitre il faut voir le numéro 15 de la liste des 10 000 mots.
On peut vérifier cela en affichant la premiere critique :
print(train_data[0])[1, 14, 22, …, 19, 178, 32]
Vérifier nos données
On peut aussi traduire, décoder ces critiques pour les lire en anglais.
Pour cela on charge le word_index, c’est un dictionnaire qui contient 88 584 mots (les 10 000 mots les plus fréquents que l’on a charger sont tirés de ce dictionnaire).
word_index = imdb.get_word_index()Ce dictionnaire contient donc 88 584 mots et un index/numéro pour chaque mot.
Si on reprend notre exemple précédent pour décoder le chiffre 15, il faut regarder dans le word_index le mot correspondant au chiffre 15.
On peut afficher les 5 premiers mots du dictionnaire :
list(word_index.items())[:5]On obtient : [(‘fawn’, 34701), (‘tsukino’, 52006), (‘nunnery’, 52007), (‘sonja’, 16816), (‘vani’, 63951)]
Pour plus de commodité et de rapidité dans le décodage on va inverser le dictionnaire pour avoir l’index à gauche et le mot à droite.
reverse_word_index = dict([(value, key) for (key, value) in word_index.items()])On ré-affiche les 5 premiers mots pour voir le changement :
list(reverse_word_index.items())[:5][(34701, ‘fawn’), (52006, ‘tsukino’), (52007, ‘nunnery’), (16816, ‘sonja’), (63951, ‘vani’)]
On peut ensuite décoder les critiques.
Ici, pour chaque chiffre dans une critique on regarde son index dans le dictionnaire.
On récupère les mot associés aux index.
Puis on joint chacun de ces mots pour faire une phrase.
decoded_review = ' '.join([reverse_word_index.get(i - 3, '?') for i in train_data[0]])
print(decoded_review)La critique décodée : « this film was just brilliant casting location scenery story direction everyone’s really suited… »
On peut aussi voir le label associé. La critique est :
- positive si le label vaut 1
- négative si le label vaut 0
print(train_labels[0])Preprocessing: One-hot encoding – Classification Binaire NLP
Malgré que les critiques soient déjà encodés numériquement il nous faut faire un deuxième traitement, un deuxième encodage.
Nous allons faire ce qu’on appelle un hot-one encoding.
C’est un encodage très utilisé en NLP, dans le traitement de texte.
Le hot-one encoding consiste à prendre en compte tous les mots qui nous intéressent (les 10 000 mots les plus fréquents). Chaque critique sera donc une liste de longueur 10 000 et si un mot apparaît dans la critique on l’encode en 1 sinon en 0.
Par exemple, encoder la séquence [3, 5] nous donnerai un vecteur de longueur 10 000 qui sera constitué de 0 à l’exception des indices 3 et 5, qui seront des 1.
Cela permettra au modèle d’apprendre plus rapidement et plus facilement.
On va donc coder la fonction vectorize_sequences pour encoder en one-hot :
import numpy as np
def vectorize_sequences(sequences, dimension=10000):
results = np.zeros((len(sequences), dimension))
for i, sequence in enumerate(sequences):
results[i, sequence] = 1.
return resultsx_train = vectorize_sequences(train_data)
x_test = vectorize_sequences(test_data)On peut ensuite afficher le premier élément du x_train pour voir concrètement le one-hot encoding.
print(x_train[0])[0. 1. 1. ... 0. 0. 0.]
Ici on modifie le type des labels en float32 à la place de int64 (notre x_train et x_test étant eux aussi en format float), pour plus de détails sur les types vous pouvez consulter cet article.
y_train = np.asarray(train_labels).astype('float32')
y_test = np.asarray(test_labels).astype('float32')Créer notre modèle de Deep Learning – Classification Binaire NLP
Structurer
Pour cette classification nous avons une configuration très simple des données:
- Les données d’entrées en liste de 1 et de 0
- Les données à prédire 1 ou 0
Le type de réseau utile dans ce cas est un empilement de couches Dense, qu’on appelle encore couches fully-connected, car tous les neurones sont reliés à tous les précédent. Ils sont totalement connectés (voir cet article pour plus d’informations sur les neurones).
On utilise par contre des fonctions d’activation différentes.
- relu pour les deux premières
- sigmoïd pour la dernière
Un article entier sera redigé sur ces fonctions d’activation. Pour le moment il suffit juste de savoir que la fonction sigmoïd permet d’avoir une probabilité entre 0 et 1.
Ainsi plus le résultat sera proche de 1 plus la critique sera positive et inversement.
from keras import models
from keras import layers
model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))Pour bien comprendre ce qu’il se passe dans ce modèle on peut regarder le schèma associé grâce à la fonction plot_model().
On peut notamment voir le changement de dimension qui s’opère sur nos données en regardant sur la partie droite de chaque couche.
Ainsi, on commence avec une liste de 10 000 mots (one-hot encoded) donc une liste de longueur 10 000.
Puis la première couche Dense applique une transformation et produit une liste de longueur 16.
La deuxième couche applique aussi une transformation pour produire une liste de longueur 16.
Et enfin, la dernière couche applique une transformation qui produit une probabilité entre 0 et 1, donc un seul chiffre, une seule dimension.
Au fait, si ton objectif est d'apprendre le Deep Learning - j’ai préparé pour toi le Plan d’action pour Maîtriser les Réseaux de neurones.
7 jours de conseils gratuits d’un ingénieur spécialisé en Intelligence Artificielle pour apprendre à maîtriser les réseaux de neurones à partir de zéro :
- Planifie ton apprentissage
- Structure tes projets
- Développe tes algorithmes d’Intelligence Artificielle
J’ai basé ce programme sur des faits scientifiques, des approches éprouvées par des chercheurs mais également mes propres techniques que j'ai conçues au fil de mes expériences dans le domaine du Deep Learning.
Pour y accéder, clique ici :
À présent, on peut revenir à ce que je mentionnais précédemment.
from keras.utils.vis_utils import plot_model
plot_model(model, to_file='model_plot.png', show_shapes=True, show_layer_names=True)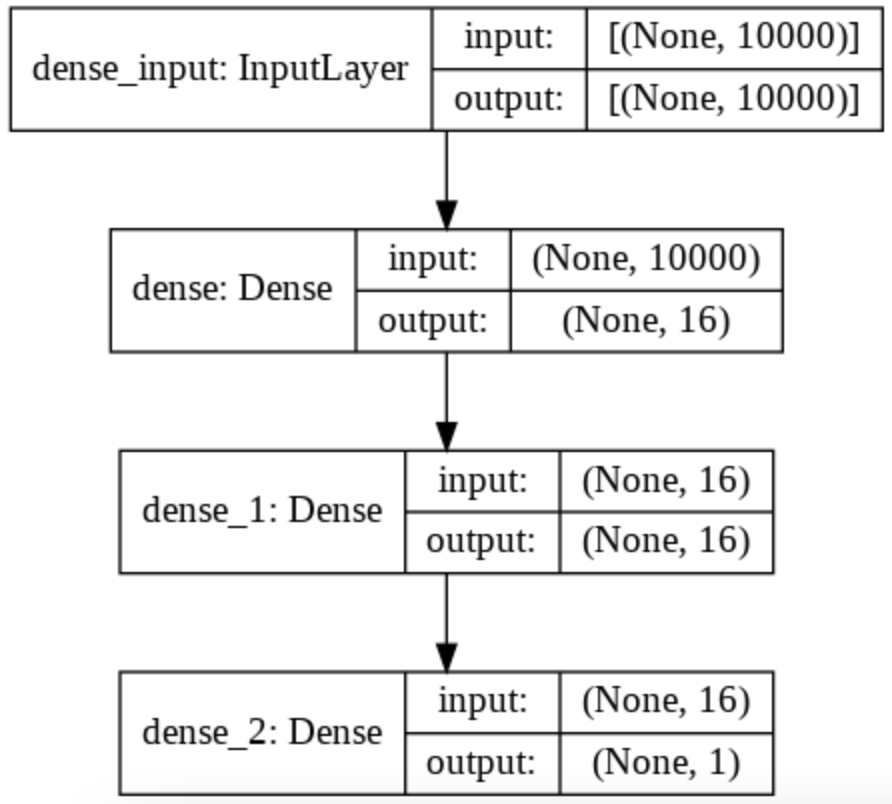
Entraîner
Dernière préparation avant d’utiliser le modèle.
Il faut séparer ces données en deux types :
- les données d’entraînement vont servir à entraîner le modèle
- les données de validation vont valider son apprentissage
En fait, cela permet d’éviter un problème fréquent en Machine Learning: l’overfitting.
L’overfitting, c’est le fait qu’un modèle se spécialise tellement sur ses données d’apprentissage qu’il devient inefficace sur d’autres données, des données réelles. On appelle aussi ce phénomène le surapprentissage.
C’est comme si vous vous entrainiez tous les jours au tennis mais seulement de votre revers. Dans un match réel vous serez très performant sur vos revers mais vos coups droits ne seront pas si bon..
L’idée c’est de bien entraîner notre modèle sur des données générales et de ne pas le surentraîner.
Le x_train de base est composés de 25 000 listes, chacune de longueur 10 000.
On sépare ces données ainsi:
- 15 000 listes pour les données d’entraînement
- 10 000 listes pour les données de validation
x_val = x_train[:10000]
partial_x_train = x_train[10000:]
y_val = y_train[:10000]
partial_y_train = y_train[10000:]On peut ensuite compiler le modèle en choisissant l’optimizer, la loss function et la métrique.
Puis entraîner le modèle avec la fonction fit().
La variable history nous permet de garder l’historique de l’apprentissage.
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['accuracy'])
history = model.fit(partial_x_train,
partial_y_train,
epochs=20,
batch_size=512,
validation_data=(x_val, y_val))
Évaluer
Dans la variable history on a les valeurs de la loss et de l’accuracy, la perte et la précision.
history_dict = history.history
history_dict.keys()Nous allons tracer un graphe avec ces valeurs pour analyser l’apprentissage de notre modèle.
import matplotlib.pyplot as plt
history_dict = history.history
loss_values = history_dict['loss']
val_loss_values = history_dict['val_loss']
epochs = range(1, len(loss_values) + 1)
plt.plot(epochs, loss_values, 'bo', label='Training loss')
plt.plot(epochs, val_loss_values, 'b', label='Validation loss')
plt.title('Training and validation loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()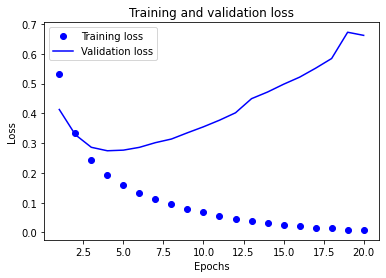
On voit au niveau des premiers epoch que la perte sur les données d’entraînement et celle sur les données de validation diminue de manière similaire.
Très vite les courbes ne diminue plus aussi vite (ce qui est normal) et à un moment, à l’epoch 4, la perte sur les données de validation augmente et ne rebaisse plus.
C’est exactement là qu’est l’overfitting.
Le modèle se spécialise sur les données d’entraînement donc la loss ne fait que diminuer pour ces données mais en se spécialisant autant il n’est plus capable d’être performant sur les données de validation et, du manière générale, sur les données réelles.
On peut d’ailleurs vérifier ce fait en traçant la courbe de la précision du modèle sur les données d’entraînement et sur les données de validation.
Effectivement, la précision diminue à partir de l’epoch 4 pour les données de validation alors qu’elle continue d’augmenter pour les données d’entraînement.
plt.clf()
acc_values = history_dict['accuracy']
val_acc_values = history_dict['val_accuracy']
plt.plot(epochs, acc_values, 'bo', label='Training accuracy')
plt.plot(epochs, val_acc_values, 'b', label='Validation accuracy')
plt.title('Training and validation accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()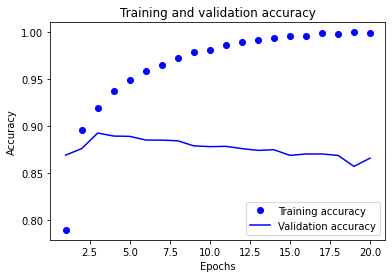
On peut aussi evaluer notre modèle sur les données de test.
On a à gauche la perte et à droite la précision.
Ici attention à ne pas confondre les deux métriques:
- la précision peut etre prise en pourcentage, si elle est de 0,85 alors 85%
- la perte elle n’est pas un pourcentage, notre but est seulement de la faire tendre vers 0
model.evaluate(x_test, y_test)[0.7295163869857788, 0.8501999974250793]
Après cette analyse, on peut améliorer notre modèle.
Améliorer
On a vu que le modèle apprend très bien sur les données d’entraînement mais moins bien sur les données de validation.
Notre modèle atteind son pic de performance à l’epoch 4.
Qu’à cela ne tienne ! On va réduire le nombre d’epoch pour améliorer la performance de notre modèle !
model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['accuracy'])
model.fit(x_train, y_train, epochs=4, batch_size=512)
results = model.evaluate(x_test, y_test)
Et voilà ! On peut évaluer à nouveau notre modèle sur les données de test pour voir l’amélioration qui a eu lieu sur la perte (plus basse) et sur la précision (plus haute).
print(results)[0.2913535237312317, 0.8844799995422363]
Pour utiliser le modèle sur de nouvelles données, rien de plus simple, il faut utiliser la fonction predict().
Cela va générer la probabilité que les critiques soient positives.
model.predict(x_test[0:2])La première critique a une probabilité de 0.20192459 d’être positive, elle est donc sûrement négative.
La deuxième critique a une probabilité de 0.99917173 d’être positive, le modèle est presque certain que la critique est positive.
Pour aller plus loin…
Le Deep Learning c’est avant tout de la pratique ! Il n’y a pas de secret théorique qui vous permettra d’améliorer la précision d’un modèle.
Augmenter la performance de son modèle c’est des tests, des expérimentations et du bidouillage.
N’hésitez pas à ajouter des couches de neurones, changer les différents hyperparamètres pour voir les changements que cela opére sur les résultats du modèle.
Ici en modifiant la dimension de la premiere couche Dense, la loss function, le batch_size et les epochs on obtient un modèle plus performant !
model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))
model.compile(optimizer='rmsprop',
loss='mse',
metrics=['accuracy'])
model.fit(x_train, y_train, epochs=3, batch_size=256)
results = model.evaluate(x_test, y_test)
Notre modèle de Classification Binaire NLP obtient une accuracy de 87% !
Grâce à notre réseau de neurones, nous avons créer une IA obtenant un haut degré de précision.
Le Deep Learning est une approche puissante ! 🚀
Ce n’est pas pour rien que Google, Amazon, Meta et OpenAI utilise cette technologie pour créer les Intelligences Artificielles de demain.
Si tu veux approfondir tes connaissances dans le domaine, tu peux accéder à mon Plan d’action pour Maîtriser les Réseaux de neurones.
Un programme de 7 cours gratuits que j’ai préparé pour te guider dans ton parcours pour apprendre le Deep Learning.
Pour y accéder, clique ici :
Un dernier mot, si tu veux aller plus loin et apprendre le Deep Learning - j’ai préparé pour toi le Plan d’action pour Maîtriser les Réseaux de neurones.
7 jours de conseils gratuits d’un ingénieur spécialisé en Intelligence Artificielle pour apprendre à maîtriser les réseaux de neurones à partir de zéro :
- Planifie ton apprentissage
- Structure tes projets
- Développe tes algorithmes d’Intelligence Artificielle
J’ai basé ce programme sur des faits scientifiques, des approches éprouvées par des chercheurs mais également mes propres techniques que j'ai conçues au fil de mes expériences dans le domaine du Deep Learning.
Pour y accéder, clique ici :




