Codons ensemble un algorithme de Deep Learning from Scratch

Aujourd’hui, nous allons voir ensemble ce qu’il se passe à l’intérieur d’un modèle de Deep Learning en le codant depuis zéro.

On va détailler, étape par étape, le processus qui s’active lorsque l’on fait du Deep Learning.

Pour rester aussi clair que possible et comprendre le principe du Deep Learning nous allons prendre un problème simple.

C’est parti !

Première étape : le problème à résoudre !

Initialiser

Imaginons… nous nous réveillons sur une planète où la température change brusquement d’une heure à l’autre.

La faune et la flore semblent être habitué à ces fréquentes perturbations climatiques mais ce n’est pas notre cas.

À côté de nous, lors de notre réveil, se tient un sac à dos.

Au fond de ce sac, se trouve un thermomètre.

En tant que scientifique averti, c’est parfait pour nous qui voulons comprendre notre nouvel environnement. Cet objet pourrra nous aider à mesurer les variations de température et comprendre un peu plus ce qu’il se passe sur cette planète !

Problème : les températures ne sont pas en degré ! Elles sont mesurés dans une obscure unité qui nous est inconnu, le Zolta.

Heureusement, une note est accrochée au thermomètre indiquant des mesures prises en Zolta et les équivalent en Celsius.

Ainsi on a :

• En Celsius : [0.5, 14.0, 15.0, 28.0, 11.0, 8.0, 3.0, -4.0, 6.0, 13.0, 21.0]
• En Zolta : [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4]

La première chose que l’on souhaite faire, en tant que Data Sciencist, c’est analyser ces données !

Dans ce tutoriel on utilisera PyTorch, mais seulement les fonctions de bases nous seront utiles 🙂

On commence par créer des tenseurs avec nos données :

import torch

t_Celsius = [0.5,  14.0, 15.0, 28.0, 11.0,  8.0,  3.0, -4.0,  6.0, 13.0, 21.0]
t_Zolta = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4]
t_Celsius = torch.tensor(t_Celsius)
t_Zolta = torch.tensor(t_Zolta)

Visualiser

Un des points important dans un problème de Deep Learning (et de Machine Learning en général) est de visualiser les données.

En fait on veut avoir une autre représentation de cette liste de chiffres.

Cela peut nous permettre de récupérer des indices sur notre problème.

On utilise matplotlib pour afficher ces données :

import matplotlib.pyplot as plt

plt.plot(t_Celsius,t_Zolta, ".")
plt.show()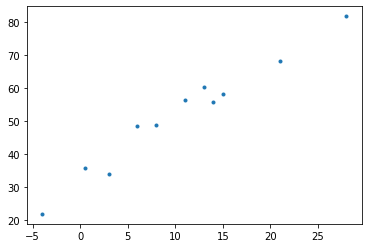

C’est bien beau ce schèma mais.. qu’est-ce qu’il signifie ?

En fait, l’idée est d’afficher les températures en Celsius en fonction des températures en Zolta et d’essayer de repérer un pattern, une répétition… quelque chose qui donnerait du sens à ces données.

Vous le voyez ?

En regardant de plus près, on peut voir que cet amas de température forme une sorte de droite.

Il est en fait aisé de résoudre ce problème. Effectivement il suffit de tracer une droite traversant cet amas de point; puis au niveau de chaque température en Zolta, se réfèrer à la droite puis observer le résultat en Celsius.

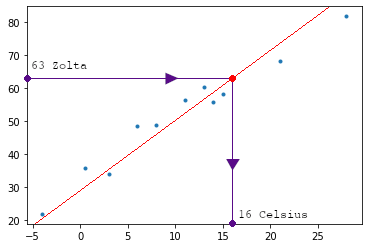
Mais l’idée ici n’est pas de résoudre le problème. Ce que nous voulons c’est comprendre le fonctionnement du Deep Learning et comment il va trouver une solution par lui-même !

Deuxième étape : le fameux modèle

Le modèle

On a donc deux séries de mesures, l’une en Celsius, l’autre en Zolta.

Par exemple :

• 35.7 Zolta = 0.5 Celsius
• 55.9 Zolta = 14 Celsius

Une mesure en Zolta équivaut à une mesure en Celsius.

En mathétique il existe un moyen très simple d’établir un lien entre deux séries de mesures (ici deux tenseurs).

Si l’on connait x et que l’on cherche à connaître sa relation avec y, cela veut dire qu’on veut trouver ce qui a permis de passer de x à y. On veut trouver le changement qui a eu lieu en x pour qu’il se transforme en y.

En langage mathématique, cela revient à chercher a et b tel que :

y = a * x + b

On dit ainsi que ces mesures sont liées linéairement.

On peut adapter ce modèle de solution à notre problème, c’est-à-dire qu’en multipliant t_Zolta par un facteur et en ajoutant une constante, nous pouvons obtenir la température en degrés Celsius.

t_Celsius = a * t_Zolta + b

Par exemple pour 35.7 Zolta = 0.5 Celsius, on aura :

0.5 = 0.01 * 35.7 + 0.15

En Deep Learning ces constantes ont des noms bien spécifique : le poids et le biais; en anglais weight et bias.

On les note donc w et b pour weight et bias :

t_Celsius = w * t_Zolta + b

Ainsi avec cette approche, on peut définir notre modèle :

def model(t_Zolta, w, b):
 return w * t_Zolta + b

La loss function

On a donc un modèle qui prend w et b en entrée et l’applique à t_Zolta pour obtenir un résultat, une « prédiction« .

Le problème c’est que si w et b ne sont pas bon, la prédiction ne sera pas bonne non plus !

Notre objectif est donc de trouver w et b pour que notre prédiction soit la plus proche possible de t_Celsius.

Il faut mesurer à quel point notre prédiction est éloignée de t_Celsius, puis changer w et b pour s’en rapprocher.

Pour mesurer l’éloignement en notre prédiction (qu’on appelle t_Pred) et t_Celsius on utilise la loss function. Littéralement : fonction de perte, elle permet de calculer l’erreur, la différence entre t_Pred et t_Celsius.

Différentes loss function existent.

Nous avons une seule contrainte : que la loss function retourne un résulat supérieur à zéro.

Restons dans la simplicité, deux options s’offre à nous :

• |t_Pred – t_Celsius|
• (t_Pred – t_Celsius)²

La deuxième options est appelée erreur quadratique moyenne ou mean square loss. C’est celle-là que nous choississons, nous allons expliqué pourquoi dans la partie suivante sur le Gradient.

On code donc notre loss function :

def loss_fn(t_Pred, t_Celsius):
 squared_diffs = (t_Pred - t_Celsius)**2
 return squared_diffs.mean()

On peut déjà commencer à voir ce que donne notre modèle avec des poids et biais par défaut (respectivement à 1 et 0).

w = torch.ones(())
b = torch.zeros(())

t_Pred = model(t_Zolta, w, b)
t_Pred

loss = loss_fn(t_Pred, t_Celsius)
loss

Une loss de 1763 c’est énorme ! Notre but maintenant, va être de réduire au minimum cette loss.

Le Gradient

Le Gradient, c’est le cœur du Deep Learning !

C’est ce qui va permettre à notre modèle d’apprendre par lui-même.

Comme dit précédemment, nous voulons réduire la loss. Pour ça il faut changer les poids et les biais, les modifier pour que notre prédiction soit plus proche de la vérité.. et il y a une manière bien précise de le faire : le Gradient.

En fait c’est une méthode bien connue en mathématique. Elle sert à optimiser un problème, une fonction.

Pour résoudre notre problème il faut que l’on sache comment et à quel point modifier w et b pour minimiser la loss.

C’est exactement l’information que nous obtenons avec le gradient.

Le gradient c’est un vecteur contenant les dérivés de la loss function par rapport à chacun des paramètres. 

Dans un modèle comportant deux paramètres ou plus, comme le nôtre, on calcule les dérivées individuelles de la loss par rapport à chaque paramètre et on les regroupe dans une variable : le gradient.

Le gradient contiendra donc un élèment pour chaque paramètre.

Chacun de ces élèments sera la dérivée de la loss par rapport à un paramètre.

C’est pour cela que nous avons choisis comme loss function le mean square loss : sa dérivé est aisément calculable !

On définit donc les dérivées :

• de la loss function
• du modèle selon w
• du modèle selon b

def dloss_fn(t_Pred, t_Celsius):
 dsq_diffs = 2 * (t_Pred - t_Celsius) / t_Pred.size(0)
 return dsq_diffs

def dmodel_dw(t_Zolta, w, b):
 return t_Zolta

def dmodel_db(t_Zolta, w, b):
 return 1.0

On peut ensuite créer la fonction du Gradient où l’on calcule tout d’abord la dérivé de la loss function.

Puis, pour chaque paramètre, on multiplie la dérivée de la loss et la dérive du modèle en fonction d’un paramètre (dans notre cas w et b).

La sortie sera un vecteur contenant le résultat de ces dérivées, c’est le gradient.

def grad_fn(t_Zolta, t_Celsius, t_Pred, w, b):
 dloss_dtp = dloss_fn(t_Pred, t_Celsius)
 dloss_dw = dloss_dtp * dmodel_dw(t_Zolta, w, b)
 dloss_db = dloss_dtp * dmodel_db(t_Zolta, w, b)
 gradient_w = dloss_dw.sum()
 gradient_b = dloss_db.sum()
 return torch.stack([gradient_w, gradient_b])

Finalement le gradient nous permettra de modifier le poids et le biais :

w = w - learning_rate * gradient_w

b = b - learning_rate * gradient_b

On a ajouter un paramètre : learning rate.

Ce paramètre nous permet de décider à quel point le poids est modifié. On en parle dans la section suivante !

Étape 3 : L’entraînement du modèle

Une boucle pour les gouverner tous

La troisième étape consiste à mettre en place l’entraînement.

L’entraînement, c’est une boucle qui va répéter un certain nombre de fois les parties précédentes :

• initialisation des paramètres
• prédiction
• calcul de loss function
• calcul des gradients
• mise à jour des paramètres

Ce nombre de répétition est appelé « epoch« .

Voici la boucle d’entraînement qui nous intéresse :

for epoch in range(1, n_epochs + 1):
        w, b = params
 
        t_Pred = model(t_Zolta, w, b)  # <1>
        loss = loss_fn(t_Pred, t_Celsius)
        grad = grad_fn(t_Zolta, t_Celsius, t_Pred, w, b)  # <2>
 
        params = params - learning_rate * grad

Nous allons rajouter deux choses :

• une brique pour afficher les résultats à différents epochs (1, 2, 3, 10, 11, 99, 100, 4000, 5000)
• une brique pour prévenir d’un problème fréquent : si le learning rate n’est pas bien définit, la loss peut très vite devenir folle et augmenter de plus en plus jusqu’à l’infini. Pour éviter cela, on utilise torch.isfinite() qui vérifie si la loss a atteint cet infini pour ensuite interrompre la boucle si c’est le cas

Finalement, on obtient cette fonction :

def training_loop(n_epochs, learning_rate, params, t_Zolta, t_Celsius, print_params=True):
    for epoch in range(1, n_epochs + 1):
        w, b = params

        t_Pred = model(t_Zolta, w, b)  # <1>
        loss = loss_fn(t_Pred, t_Celsius)
        grad = grad_fn(t_Zolta, t_Celsius, t_Pred, w, b)  # <2>

        params = params - learning_rate * grad

        if epoch in {1, 2, 3, 10, 11, 99, 100, 4000, 5000}:  # <3>
            print('Epoch %d, Loss %f' % (epoch, float(loss)))
            if print_params:
                print('    Params:', params)
                print('    Grad:  ', grad)
        if epoch in {4, 12, 101}:
            print('...')

        if not torch.isfinite(loss).all():
            break  # <3>
            
    return params

Après avoir définit notre fonction, on peut l’utiliser.

On prend :

• 100 epoch
• learning rate de 0.0001
• poids de 1
• biais de 0

En retour, la fonction affichera l’évolution de la loss, des poids et biais, et du Gradient !

training_loop(
    n_epochs = 100,
    learning_rate = 1e-4,
    params = torch.tensor([1.0, 0.0]),
    t_Zolta = t_Zolta,
    t_Celsius = t_Celsius)

Epoch 1 :

• Loss 1763.884766
• Params: tensor([ 0.5483, -0.0083])
• Grad: tensor([4517.2964, 82.6000])

Epoch 100 :

• Loss 29.022667
• Params: tensor([ 0.2327, -0.0438])
• Grad: tensor([-0.0532, 3.0226])

Le gradient, à la première epoch, a un poids environ 50 fois plus grand que le gradient pour le biais.

Cela signifie que le poids et le biais évoluent sur des échelles différentes.

Si c’est le cas, un learning rate suffisamment important pour mettre à jour l’un sera si important qu’il sera instable pour l’autre; à l’inverse, un learning rate approprié pour l’autre ne sera pas suffisamment important pour modifier significativement le premier.

Normaliser les données

Nous pouvons nous assurer que les données d’entrée ne s’éloigne pas trop de l’échelle -1,0 à 1,0.

Dans notre cas, on peut obtenir quelque chose de convenable en multipliant simplement t_Zolta par 0,1.

t_Zolta_n = 0.1 * t_Zolta

training_loop(
    n_epochs = 100,
    learning_rate = 1e-2,
    params = torch.tensor([1.0, 0.0]),
    t_Zolta = t_Zolta_n,
    t_Celsius = t_Celsius)

Epoch 1 :

• Loss 171.868347
• Params: tensor([1.1461, 0.2100])
• Grad: tensor([-14.6089, -21.0000])

Epoch 100 :

• Loss 6.498067
• Params: tensor([7.7523, 9.1075])
• Grad: tensor([-2.3752, -2.8419])

Voilà ! Les gradients ont une amplitude similaire.

L’utilisation d’un seul learning rate pour les deux paramètres fonctionne alors très bien.

Nous pourrions probablement faire un meilleur travail de normalisation qu’une simple multiplication par 0.1, mais puisque cela fonctionne, nous allons nous en contenter pour le moment 🙂

Étape 4 : Le résultat

Obtenir les résultats

Nous allons finalement faire notre entraînement sur 5000 epoch pour voir ce que notre modèle a dans le ventre !

params = training_loop(
    n_epochs = 5000,
    learning_rate = 1e-2,
    params = torch.tensor([1.0, 0.0]),
    t_Zolta = t_Zolta_n,
    t_Celsius = t_Celsius,
    print_params = False)

On affiche les nouveaux poids et biais :

params

On obtient : tensor([ 5.3671, -17.3012])

Les valeurs de w et b ressemblent beaucoup aux nombres que nous devons utiliser pour convertir les degrés Celsius en degrés Fahrenheit. Les valeurs exactes seraient w = 5,5556 et b = -17,7778.

Les Zolta étaient en fait des Fahrenheit pendant tout ce temps. Pas de grande découverte, si ce n’est que notre processus de Deep Learning fonctionne !

Visualiser les résultats

Pour afficher les résultats, on va se servir de la librairie matplotlib.

On va aussi utiliser une astuce Python appelée arguments unpacking avec *params. Cela veut dire que l’on prend les éléments du tenseur params comme des arguments indépendants.

En Python, cela se fait généralement avec des listes ou des tuples, mais nous pouvons également utiliser l’arguments unpacking avec les tenseurs PyTorch, qui seront séparé selon la dimension principale.

Donc ici, model(t_Zolta_n, *params) est équivalent à model(t_Zolta_n, params[0], params[1]).

%matplotlib inline
from matplotlib import pyplot as plt

t_Pred = model(t_Zolta_n, *params)

fig = plt.figure(dpi=100)
plt.xlabel("Temperature (°Fahrenheit)")
plt.ylabel("Temperature (°Celsius)")
plt.plot(t_Zolta.numpy(), t_Pred.detach().numpy())
plt.plot(t_Zolta.numpy(), t_Celsius.numpy(), 'o')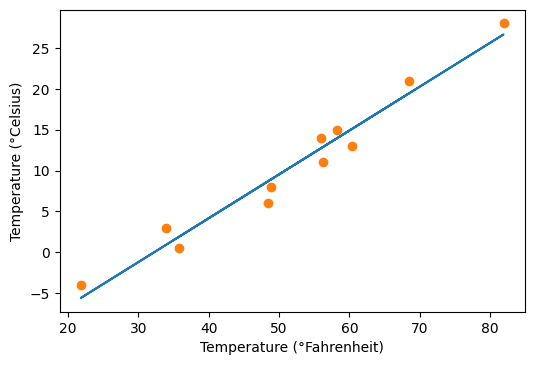

La boucle est bouclée. On a bien une droite passant au milieu de cet amas de point, comme expliqué au début.

On va pouvoir continuer l’exploration de cette planète !

sources :

• L. Antiga, Deep Learning with PyTorch (2020, Manning Publications) – notre lien affilié
• Photo by NASA on Unsplash